Rymano dzeta funkcija

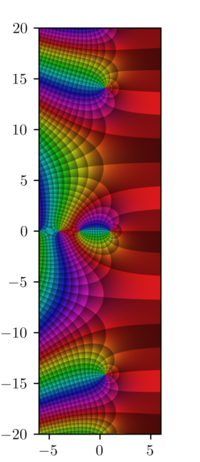
Rymano dzeta funkcija (kai kur Oilerio ir Rymano dzeta funkcija), – Dirichlė eilutės sumos analizinis plėtinys, kompleksinio argumento s (realioji s dalis >1) funkcija:
Rymano dzeta funkcija yra kertinis skaičių teorijos akmuo, turi daug taikymų fizikoje, tikimybių teorijoje, statistikoje.
Šią funkciją, tiesa realaus argumento, aštuoniolikto amžiaus pradžioje pirmasis nagrinėjo Leonardas Oileris. Bernhardas Rymanas 1859 m. straipsnyje apie pirminių skaičių pasiskirstymą praplėtė funkcijos apibrėžimą į kompleksinio argumento sritį, įrodė, kad ji yra meromorfinė funkcija bei nustatė sąryšius tarp jos nulių ir pirminių skaičių asimptotinio pasiskirstymo.[2]
Rymano dzeta funkcijos vertes argumentams esant teigiamiems lyginiams skaičiams apskaičiavo L. Oileris. Pirmoji jų, būtent, , yra Bazelio problemos sprendinys. 1979 m. prancūzų matematikas Apéry įrodė iracionalumą (Šis skaičius vėliau buvo pavadintas jo vardu). L. Oileris taip pat surado, kad funkcijos reikšmės, esant neigiamoms sveikosioms argumento vertėms yra racionalieji skaičiai. Jos vaidina svarbų vaidmenį moduliarinių formų teorijoje. Šiuo metu yra pasiūlyta daug Rymano dzeta funkcijos apibendrinimų, pvz., Dirichlė eilutė, Dirichlė L-funkcija, L-funkcijos.
Apibrėžimas
[redaguoti | redaguoti vikitekstą]
Rymano dzeta funkcija yra kompleksinio kintamojo funkcija.
Begalinė skaičių eilutė konverguoja visoms vertėms, kurių realioji dalis > 1:
Ji taip pat gali būti užrašyta kaip
- ,
čia
yra Gama funkcija.
1740 metais Leonardas Oileris šią eilutę nagrinėjo esant sveikiesiems teigiamiems , o Pafnutijus Čebyšovas praplėtė ją visiems realiems argumentams su .[3]
Rymanas parodė, kad šios eilutės apibrėžimo sritis gali būti analiziškai išplėsta visiems kompleksiniams . Kai , ši eilutė yra vadinama harmonine eilute, ji diverguoja link , ir
Taigi, Rymano dzeta funkcija yra meromorfinė funkcija visoje kompleksinėje -plokštumoje. Ji yra holomorfinė funkcija visur, išskyrus pirmos eilės polių su reziduumu 1.
Kai kurios Rymano dzeta funkcijos vertės
[redaguoti | redaguoti vikitekstą]
Bet kokiam lyginiam sveikam argumentui :
Čia yra eilės Bernulio skaičiai.
Nelyginiams teigiamiems sveikiesiems skaičiams nėra žinomos panašios paprastos išraiškos, tačiau manoma, kad funkcijos vertės turi būti susijusios su algebrine -sveikųjų skaičių teorija (taip vadinamomis L-funkcijų specialiosiomis vertėmis).
Neigiamiems sveikiesiems skaičiams turime
dėl (naudojami žymėjimai )
yra lygu nuliui visiems neigiamiems lyginiams sveikiems skaičiams, kadangi visiems nelyginiams , išskyrus 1.
Panaudojant analizinį plėtinį galima parodyti, kad:
- Tai leidžia priskirti baigtinę vertę diverguojančiai eilutei , kuri dažnai naudojama stygų teorijoje.[4]
- Panašiai samprotaujant tokiu būdu priskiriama baigtinė vertė ir eilutei .
- jei mes artėsime prie 1 iš didesnių skaičių pusės. Tai yra vadinamoji harmoninė eilutė. Tačiau jos suma Koši prasme
- yra baigtinis skaičius, vadinamas Oilerio-Maskeronio konstanta .
- jei mes artėsime prie 1 iš didesnių skaičių pusės. Tai yra vadinamoji harmoninė eilutė. Tačiau jos suma Koši prasme
- Ši vertė naudojama skaičiuojant Boze–Einšteino kondensato kritinę temperatūrą uždarame tūryje su periodinėmis kraštinėmis sąlygomis bei įmagnetėjimo bangų sklidimą nelaidžiose aplinkose.
- Ši lygybė yra taip vadinama Bazelio problema. Atvirkštinis šiai sumai skaičius atsako į klausimą: Kokia tikimybė, kad du atsitiktinai pasirinkti teigiami sveikieji skaičiai turės didžiausią bendrąjį daliklį lygų tik 1?[5]
- Tai yra Apéry konstanta. Atvirkštinis šiai sumai skaičius atsako į klausimą: Kokia tikimybė, kad trys atsitiktinai pasirinkti teigiami sveikieji skaičiai turės didžiausią bedrąjį daliklį lygų 1?
- Šis skaičius gaunamas išvedant Stefano ir Bolcmano spinduliuotės dėsnį fizikoje – integruojant Planko spinduliuotės dėsnį.
Oilerio begalinė sandauga
[redaguoti | redaguoti vikitekstą]Vieną įdomiausių skaičių teorijos sąryšių tarp dzeta funkcijos ir pirminių skaičių atrado L. Oileris, įrodęs tapatybę:
čia kairėje pusėje yra , o dešinėje pusėje yra begalinė sandauga pagal visus pirminius skaičius :
Oilerio tapatybė įrodoma naudojant tik geometrinės progresijos eilutę ir pagrindinę aritmetikos teoremą. Kadangi harmoninė eilutė (gauta kai ) diverguoja, iš Oilerio tapatybės () seka, kad yra be galo daug pirminių skaičių.[6]
Oilerio sandauga gali būti naudojama skaičiuojant tikimybę, kad atsitiktinai pasirinktų teigiamų sveikųjų skaičių tarpusavyje turės didžiausią bendrąjį daliklį 1. Nesunku įsitikinti, kad tikimybė, jog atsitiktinai paimtas skaičius dalinsis iš skaičiaus yra . Tuomet tikimybė, kad skaičių dalinsis iš šio skaičiaus bus , o tikimybė, kad bent vienas iš jų nesidalins bus . Kadangi šie (dalinimo) įvykiai yra nepriklausomi, atsakymas bus jų sandauga. Taigi, galutinai turėsime tokią asimptotinę tikimybę:[7],
Funkcinės lygtys
[redaguoti | redaguoti vikitekstą]Rymano dzeta funkcija įeina į daugelį funkcinių sąryšių, pvz.:
čia yra Gama funkcija, o pati lygtis yra vadinama Rymano funkcine lygtimi. Ji susieja funkcijos vertes taškuose ir . Sinusinis narys reiškia, kad turi paprastus nulius ties lyginiais neigiamais skaičiais – jie yra žinomi kaip trivialieji funkcijos nuliai. Kai yra lyginis teigiamas skaičius, sandauga dešinėje lygties pusėje yra nenulinė, kadangi taške yra paprastas polius, o sinuso funkcija tame taške yra paprastas nulis.
Šią tapatybę 1859 metais išvedė Rymanas. Tačiau analogišką sąryšį, tiesa, be įrodymo, jau 1749 metais buvo pateikęs ir L. Oileris Dirichlė funkcijai (dzeta funkcija su alternuojančiais nariais):
Tai leidžia įvertinti srityje, t. y.
Rymanas taip pat surado simetrinę funkcinės lygties versiją įvedus pažymėjimą:
Šiai funkcinei lygčiai galioja:
Nuliai, kritinė linija, Rymano hipotezė
[redaguoti | redaguoti vikitekstą]

Iš anksčiau minėtos funkcinės lygties seka, kad Rymano dzeta funkcija turi nulius —2, —4,…. Tai yra trivialieji nuliai, taip vadinami, kadangi jų argumentų reikšmes galima paprastai rasti iš funkcinės lygties ( yra 0). Netrivialieji nuliai yra įdomesni ne tik tuo, kad jų pasiskirstymas ne iki galo suprastas. Jų tyrimai davė daug įdomių rezultatų apie pirminius skaičius. Yra žinoma, kad netrivialieji nuliai yra randami juostoje , kuri yra vadinama kritine juosta. Įžymioji Rymano hipotezė teigia, kad bet kuris netrivialusis nulis turi . Rymano dzeta funkcijos teorijoje aibė yra vadinama kritine linija. Rymano dzeta funkcijos dalis išilgai kritinės linijos yra vadinama Z funkcija.
Hardy ir Littlewood hipotezė
[redaguoti | redaguoti vikitekstą]1914 metais Godfrey Harold Hardy įrodė, kad turi be galo daug netrivialiųjų nulių.
Hardy ir John Edensor Littlewood suformulavo du spėjimus apie nulių išsidėstymo tankį ir atstumus tarp nulių. Toliau, yra bendras nulių skaičius esant realiesiems argumentams, o yra bendras funkcijos nelyginės eilės nulių skaičius esantis intervale .
Kiekvienam , egzistuoja toks , kad
intervale yra nelyginės eilės nulis. Bet kokiam egzistuoja ir tokie, kad nelygybė
yra teisinga, kai
- .
Atvirkštinė funkcija
[redaguoti | redaguoti vikitekstą]Vienetas, padalintas iš dzeta funkcijos gali būti užrašytas Dirichlė eilute panaudojant Miobijaus funkciją :
visiems kompleksiniams kurių realioji dalis didesnė už 1.
Sąryšiai su kitomis funkcijomis
[redaguoti | redaguoti vikitekstą]Dirichlė eilutė
[redaguoti | redaguoti vikitekstą]Kiek pertvarkius Rymano dzeta funkciją, galima išplėsti jos konvergavimo sritį.[8] Taip eilutė
konverguoja srityje , o
konverguoja net . Panašiai konverguojančią eilutę galima gauti dėl bet kokio neigiamo .
Melino transformacijos
[redaguoti | redaguoti vikitekstą]Funkcijos Melino transformacija apibrėžiama taip:
Yra daug dzeta funkcijos sąryšių su Melino transformacija. Pavyzdžiui, kai realioji dalis didesnė už 1, turėsime
kur žymi gama funkciją. Modifikavęs integravimo kontūrą, Rymanas parodė, kad
visiems (čia pažymėtas Hankelio kontūras).
Rymano dzeta funkciją taip pat galima susieti su pirminių skaičių pasiskirstymo funkcija :
vertėms .
Įvedus funkciją
galima parodyti, kad
Šios lygtys gali būti naudojamos analizuojant pirminių skaičių pasiskirstymą. gali būti atstatyta, panaudojus Miobijaus transformaciją.
Theta funkcijos
[redaguoti | redaguoti vikitekstą]Rymano dzeta funkcija taip pat gali būti susieta su funkcija per Melino transformaciją[9]
Čia
Lorano eilutė
[redaguoti | redaguoti vikitekstą]Rymano dzeta funkcija yra meromorfinė funkcija su pirmos eilės poliumi esant argumentui . Taigi, ji gali būti išskleista Lorano eilute su poliumi :
Konstantos yra vadinamos Stiljeso konstantomis. Jos apibrėžiamos formulėmis:
yra Oilerio-Maskeronio konstanta.
Integralas
[redaguoti | redaguoti vikitekstą]Visiems kompleksiniams galioja integralinis sąryšis:
Jis dažnai naudojamas įvertinant dzeta funkciją skaitmeniškai.[10]
Adamaro sandauga
[redaguoti | redaguoti vikitekstą]Pasinaudodamas Vejerštraso faktorizavimo teorema, Adamaras išvedė tokį dzeta funkcijos skleidinį:
Čia dauginama pagal netrivialiuosius dzeta funkcijos nulius , o žymi Oilerio-Maskeronio konstantą. Dar paprasčiau užrašomas kitas dzeta funkcijos skleidinys begaline sandauga:
Čia aiškus polius ties , trivialieji nuliai ties —2,—4,… (dėl Gama funkcijos, vardiklyje) ir netrivialieji nuliai ties .
Globaliai konverguojančios eilutės
[redaguoti | redaguoti vikitekstą]Globaliai konverguojanti dzeta funkcijos eilutę visiems kompleksiniams išskyrus taškus bet kokiam sveikam , pirmą kartą užrašė Konrad Knopp, o įrodė Helmut Hasse 1930 metais:
Nors ši eilutė buvo pateikta Hasse straipsnyje, ji nebuvo žinoma iki tol kol buvo iš naujo Jonathan Sondow atrasta po 60 metų.[11]
Hasse rado ir kitą išraišką
Tačiau ją dar Joseph Ser irgi buvo pateikęs 1926 metais.[12]
Praktiniai taikymai
[redaguoti | redaguoti vikitekstą]Rymano dzeta funkcija dažnai sutinkama statistikoje (pvz., Zipfo dėsnis).
Dzeta funkcija naudojama diverguojančių eilučių ir integralų reguliarizavimui (priskiriama baigtinė vertė šiaip jau diverguojančioms sumoms). Rymano dzeta funkcija naudojama aprašant Kazimiro efektą, dinaminių sistemų analizėje.[13]
Begalinės eilutės
[redaguoti | redaguoti vikitekstą]Rymano dzeta funkcijai galioja:[14]
Lyginių ir nelyginių dzeta funkcijos narių sumos duoda tokias vertes:
ir
Parametrizuotos aukščiau pateiktų sumų versijos gali būti užrašomos kaip:
ir
su , o ir yra poligama funkcija ir Oilerio konstanta atitinkamai. Taip pat:
- .
Galioja ir tokie sąryšiai:
- ,
kur žymi kompleksinio skaičiaus menamąją dalį.
Rymano dzeta funkcijos apibendrinimai
[redaguoti | redaguoti vikitekstą]Yra žinoma daug funkcijų, susijusių su Rymano dzeta funkcija, kurios gali būti traktuojamos kaip Rymano dzeta funkcijos apibendrinimai. Viena jų yra Hurwitz dzeta funkcija
(Konverguojančią eilutę jai pateikė Helmut Hasse 1930 metais,[15]), kuri sutampa su Rymano dzeta funkcija kai (pažymėtina, kad Hurwitz dzeta funkcijos apatinė sumavimo riba ne 1, o 0), Dirichlė L-funkcija, Dedekindo zeta-funkcija.
Vadinamoji polilogaritminė funkcija užrašoma taip:
- .
Ji sutampa su Rymano dzeta funkcija kai .
Ji sutampa su Rymano dzeta funkcija kai ir .
Clausen funkcija tai funkcija, gaunama paimant funkcijos realiąją arba menamąją dalį.
Galima įvesti daugelio kintamųjų dzeta funkciją:
Šią funkciją galima analiziškai praplėsti į -matę kompleksinių skaičių sritį.
Trupmeninė išvestinė
[redaguoti | redaguoti vikitekstą]Rymano dzeta funkcijos -eilės trupmeninė išvestinė gali būti užrašyta tokiu pavidalu [16]
Jei yra trupmena tokia, kad , konvergavimo sritis bus .
Išnašos
[redaguoti | redaguoti vikitekstą]- ↑ „Jupyter Notebook Viewer“. Nbviewer.ipython.org. Nuoroda tikrinta 2017-01-04.
- ↑ Šiame straipsnyje taip pat pateikiama įžymioji Rymano hipotezė apie dzeta funkcijos kompleksinių nulių pasiskirstymą – vienas įdomiausių neišspręstų matematikos uždavinių.Bombieri, Enrico. „The Riemann Hypothesis – official problem description“ (PDF). Clay Mathematics Institute. Suarchyvuotas originalas (PDF) 2015-12-22. Nuoroda tikrinta 2014-08-08.
- ↑ Devlin, Keith (2002). The Millennium Problems: The Seven Greatest Unsolved Mathematical Puzzles of Our Time. New York: Barnes & Noble. pp. 43–47. ISBN 978-0-7607-8659-8.
- ↑ Polchinski, Joseph (1998). String Theory, Volume I: An Introduction to the Bosonic String. Cambridge University Press. p. 22. ISBN 978-0-521-63303-1.
- ↑ Ogilvy, C. S.; Anderson, J. T. (1988). Excursions in Number Theory. Dover Publications. pp. 29–35. ISBN 0-486-25778-9.
- ↑ Sandifer, Charles Edward (2007). How Euler Did It. Mathematical Association of America. p. 193. ISBN 978-0-88385-563-8.
- ↑ Nymann, J. E. (1972). „On the probability that positive integers are relatively prime“. Journal of Number Theory. 4 (5): 469–473. Bibcode:1972JNT.....4..469N. doi:10.1016/0022-314X(72)90038-8.
- ↑ Knopp, Konrad (1945). Theory of Functions. pp. 51–55.
- ↑ Neukirch, Jürgen (1999). Algebraic number theory. Springer. p. 422. ISBN 3-540-65399-6.
- ↑ „Mathematik-Online-Kurs: Numerik-Numerische Integration-Riemannsche Zeta-Funktion“. Mo.mathematik.uni-stuttgart.de. 2010-09-09. Nuoroda tikrinta 2017-01-04.
- ↑ Sondow, Jonathan (1994). „Analytic continuation of Riemann's zeta function and values at negative integers via Euler's transformation of series“ (PDF). Proceedings of the American Mathematical Society. 120 (2): 421–424. doi:10.1090/S0002-9939-1994-1172954-7.
- ↑ Blagouchine, Iaroslav V. (2016), "Expansions of generalized Euler's constants into the series of polynomials in π?2 and into the formal enveloping series with rational coefficients only", Journal of Number Theory 158: 365–396, doi:
- ↑ „Work on spin-chains by A. Knauf, et. al“. Empslocal.ex.ac.uk. Nuoroda tikrinta 2017-01-04.
- ↑ Dauguma formulių šiame skyrelyje yra iš § 4 of J. M. Borwein et al. (2000)
- ↑ Hasse, Helmut (1930). „Ein Summierungsverfahren für die Riemannsche -Reihe“. Mathematische Zeitschrift. 32 (1): 458–464. doi:10.1007/BF01194645.
- ↑ Guariglia, E. (2015). Fractional derivative of the Riemann zeta function. In: Fractional Dynamics (Cattani, C., Srivastava, H., and Yang, X. Y.). De Gruyter. pp. 357–368. doi:10.1515/9783110472097-022.
Šaltiniai
[redaguoti | redaguoti vikitekstą]- Apostol, T. M. Zeta and Related Functions.
- Borwein, Jonathan; Bradley, David M.; Crandall, Richard (2000). „Computational Strategies for the Riemann Zeta Function“ (PDF). J. Comp. App. Math. 121 (1–2): 247–296. Bibcode:2000JCoAM.121..247B. doi:10.1016/S0377-0427(00)00336-8. Suarchyvuotas originalas (PDF) 2006-09-25. Nuoroda tikrinta 2017-12-18.
- Cvijović, Djurdje; Klinowski, Jacek (2002). „Integral Representations of the Riemann Zeta Function for Odd-Integer Arguments“. J. Comp. App. Math. 142 (2): 435–439. Bibcode:2002JCoAM.142..435C. doi:10.1016/S0377-0427(02)00358-8. MR 1906742.
- Cvijović, Djurdje; Klinowski, Jacek (1997). „Continued-fraction expansions for the Riemann zeta function and polylogarithms“. Proc. Amer. Math. Soc. 125 (9): 2543–2550. doi:10.1090/S0002-9939-97-04102-6.
- Edwards, H. M. (1974). Riemann's Zeta Function. Academic Press. ISBN 0-486-41740-9. Has an English translation of Riemann’s paper.
- Hadamard, Jacques (1896). „Sur la distribution des zéros de la fonction ?(s) et ses conséquences arithmétiques“. Bulletin de la Societé Mathématique de France. 14: 199–220.
- Hardy, G. H. (1949). Divergent Series. Clarendon Press, Oxford.
- Hasse, Helmut (1930). „Ein Summierungsverfahren für die Riemannsche -Reihe“. Math. Z. 32: 458–464. doi:10.1007/BF01194645. MR 1545177. (Globally convergent series expression.)
- Ivic, A. (1985). The Riemann Zeta Function. John Wiley & Sons. ISBN 0-471-80634-X.
- Motohashi, Y. (1997). Spectral Theory of the Riemann Zeta-Function. Cambridge University Press. ISBN 0521445205.
- Karatsuba, A. A.; Voronin, S. M. (1992). The Riemann Zeta-Function. Berlin: W. de Gruyter.
- Mez?, Istv?n; Dil, Ayhan (2010). „Hyperharmonic series involving Hurwitz zeta function“. Journal of Number Theory. 130 (2): 360–369. doi:10.1016/j.jnt.2009.08.005. MR 2564902.
- Montgomery, Hugh L.; Vaughan, Robert C. (2007). Multiplicative number theory. I. Classical theory. Cambridge tracts in advanced mathematics. 97. Cambridge University Press. Ch. 10. ISBN 0-521-84903-9.
- Newman, Donald J. (1998). Analytic number theory. Graduate Texts in Mathematics. 177. Springer-Verlag. Ch. 6. ISBN 0-387-98308-2.
- Raoh, Guo (1996). „The Distribution of the Logarithmic Derivative of the Riemann Zeta Function“. Proceedings of the London Mathematical Society. s3–72: 1–27. doi:10.1112/plms/s3-72.1.1.
- Riemann, Bernhard (1859). „Über die Anzahl der Primzahlen unter einer gegebenen Grösse“. Monatsberichte der Berliner Akademie.. In Gesammelte Werke, Teubner, Leipzig (1892), Reprinted by Dover, New York (1953).
- Sondow, Jonathan (1994). „Analytic continuation of Riemann's zeta function and values at negative integers via Euler's transformation of series“ (PDF). Proc. Amer. Math. Soc. 120 (2): 421–424. doi:10.1090/S0002-9939-1994-1172954-7.
- Titchmarsh, E. C. (1986). Heath-Brown (red.). The Theory of the Riemann Zeta Function, (2nd rev. leid.). Oxford University Press.
- Whittaker, E. T.; Watson, G. N. (1927). A Course in Modern Analysis (4th leid.). Cambridge University Press. Ch. 13.
- Zhao, Jianqiang (1999). „Analytic continuation of multiple zeta functions“. Proc. Amer. Math. Soc. 128 (5): 1275–1283. doi:10.1090/S0002-9939-99-05398-8. MR 1670846.
Nuorodos
[redaguoti | redaguoti vikitekstą]- Riemann Zeta Function, in Wolfram Mathworld – an explanation with a more mathematical approach
- Tables of selected zeros Archyvuota kopija 2009-05-17 iš Wayback Machine projekto.
- Prime Numbers Get Hitched Archyvuota kopija 2008-07-21 iš Wayback Machine projekto. A general, non-technical description of the significance of the zeta function in relation to prime numbers.
- X-Ray of the Zeta Function Visually oriented investigation of where zeta is real or purely imaginary.
- Formulas and identities for the Riemann Zeta function functions.wolfram.com
- Riemann Zeta Function and Other Sums of Reciprocal Powers, section 23.2 of Abramowitz and Stegun
- Frenkel, Edward. „Million Dollar Math Problem“ (video). Brady Haran. Nuoroda tikrinta 11 March 2014.
- Mellin transform and the functional equation of the Riemann Zeta function—Computational examples of Mellin transform methods involving the Riemann Zeta Function




































































![{\displaystyle (0,T]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/8c12e3f78f8db2b37a4aed7f654aa7a160754bd9)



![{\displaystyle (T,T+H]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/5a7f206ba185f5e71e82482b52823f9cab4a9d99)































































