Difrakcija
Difrakcija (nuo lot. „diffringere“, „skaidyti į dalis“, „sklaidyti“) – bet koks nuokrypis nuo bangų tiesaeigio sklidimo, nepaaiškinamas bangos atspindžiu arba lūžiu. Optikoje difrakcijos sąvoka yra susieta su banginėmis šviesos savybėmis ir nėra paaiškinama dalelinės šviesos teorijos rėmuose. Klasikiniuose difrakcijos eksperimentuose buvo naudojami įvairių formų plyšiai ir šviesos difrakcija vis stipriau pasireikšdavo plyšio matmenims artėjant prie šviesos bangos ilgio. Tuomet šviesa, sklisdama pro plyšį, nukrypdavo nuo tiesaus kelio, o klasikinio šešėlio sritis buvo tuo mažesnė, kuo plyšio matmuo buvo artimesnis bangos ilgiui. Analogiškai buvo stebėta šviesos difrakcija ties kliūtimi. Kuo artimesni kliūties matmenys šviesos bangos ilgiui, tuo mažesnė klasikinio šešėlio sritis už kliūties. Difrakcija buvo paaiškinta Hiugenso ir Frenelio principo pagalba. Šviesos bangos paviršius kiekvienu laiko momentu yra ne paprasta antrinių bangų gaubtinė, o tų bangų interferencijos rezultatas.
Šviesos difrakcijai vykti nėra būtinos bangos ilgio matmenų kliūtys arba plyšiai. Koherentinių šviesos šaltinių, tokių kaip lazeris, spinduliuojama šviesa difraguoja savaime. Lazerio spinduliuotei yra būdinga sudėtinga erdvinė sandara, priklausanti nuo lazerinio rezonatoriaus simetrijos bei lazerinės generacijos sąlygų. Lazeris su skirtingais lazerinio rezonatoriaus išvadiniais veidrodžiais be lazeriniu kaupinimu spinduliuoja skirtingas lazerinės spinduliuotės skersinės modas. Žemiausios eilės moda – Gauso pluoštas – yra lengviausiai sužadinama lazerio moda, turintį platų taikymą. Esminė Gauso pluošto savybė yra tą, kad jos neįmanoma sufokusuoti iki matmenų mažesnių negu bangos ilgis. Dėl šios priežasties šiuolaikinėje optikoje Gauso pluoštas ir kitos lazerinio rezonatoriaus modos yra vadinami difraguojančiais spinduliais. Difrakcija yra svarbi optinių laikmenų teorijoje, kadangi ji riboja CD/DVD arba Blu-ray Disc lazerio mažiausios dėmės matmenis, o tuo pačiu ir įrašomos informacijos kiekį. Difrakcija yra svarbi litografijoje, kadangi gaminant mikroschemų ir procesorių takelius ji riboja mažiausią pasiekiamą takelio dydį.
Regimosios šviesos bangos ilgis yra labai mažas lyginant su žmogaus akies lastelėmis, todėl jos spinduliai nukrypsta nuo tiesaus sklidimo kelio kasdien sutinkamose situacijose labai mažu kampu. Tiesiaeigio šviesos sklidimo ir kiti geometrinės optikos dėsniai pakankamai tikslūs tiktai tada, kai šviesos sklidimo kelyje esančių kliūčių matmenys yra daug didesni už šviesos bangos ilgį.


Difrakcijos pavyzdžiai kasdieniame gyvenime[redaguoti | redaguoti vikitekstą]
Difrakcijai pasireikšti yra būtini koherentiniai šviesos šaltiniai. Paprastai gamtoje retai pasitaiko situacijos, kuomet šviesos šaltinį galima vadinti koherentiniu. Tačiau Saulės šviesa savo kelyje sutikusi mažas kliūtis (vandens lašus, ledo kristalus) gali būti apytiksliai laikoma koherentinė. Kuomet šviesa susiduria ypač smulkiais vandens lašais, atmosferoje yra stebimi šviesos difrakcijos sąlygoti reiškiniai – vainikai ir rūko lankai. Vainikai yra stebimi danguje kaip spalvoti ratilai, susidarantys aplink įvairius dangaus skliaute esančių šviesos šaltinius – Saulę, Mėnulį, planetas, žvaigždes ir net debesis. Rūko lankas yra giminingas vaivorykštėms, kadangi šio efekto priežastis yra taip pat vandens lašai, bet spalvų išsidėstymas rūko lanke žymiai skiriasi nuo spalvų išsidėstymo vaivorykštėje dėl fizikinių reiškinių skirtumų. Dar vienas difrakcijos pavyzdys yra gamtoje sutinkamos difrakcinės gardelės – vorų tinklai, vabzdžių sparnai.
Atsiradus koherentiniams šviesos šaltiniams, difrakcija yra sutinkama dažniau. Paprasčiausias difrakcijos pavyzdys yra nuo optinių informacinių laikmenų atspindėjusi šviesa – CD arba DVD disko paviršiuje tvarkingai įrašyti informacijos bitai elgiasi kaip difrakcinė gardelė. Hologramos, klijuojamos ant kreditinių kortelių, taip pat yra difrakcinės gardelės pavyzdžiai. Telefono arba monitoriaus LCD matrica išjungtoje būsenoje elgiasi kaip difrakcinė gardelė – taip yra dėl skystųjų kristalų molekulių tvarkingo išsidėstymo.
Difrakcija yra būdinga bet kokioms bangoms. Vandenyno bangos difraguoja nuo paviršiuje esančių kliūčių bei plyšių. Garso bangos taip pat difraguoja nuo dujose esančių objektų.
Difrakcija informacijos perdavime[redaguoti | redaguoti vikitekstą]
Signalų laikinė bei erdvinė lokalizacija yra vienas svarbiausių veiksnių perduodant informaciją bangų pagalba. Laike lokalizuotos bangos vadinamos impulsais, o lokalizuotos erdvėje – pluoštais. Neminint kitų fizikinių procesų, ribojančių informacijos perdavimo galimybes, pagrindiniai procesai, ribojantys informacijos perdavimą pluoštų ir impulsų pagalba, yra bangų difrakcija bei dispersija. Difrakcija sąlygoja informacijos perdavime naudojamų bangų pluoštų plitimą erdvėje, pluoštų erdvinės lokalizacijos laipsnis kinta, jis visąlaik mažėja. Tuo būdu, nukenčia informaciją perduodančių bangų signalų erdvinė skyra. Bangų pluoštai nusklidę tam tikrą atstumą persikloja ir tampa nebeatskiriami, o signaluose užkoduota informacija yra prarandama. Dalinis tokio informacijos praradimo atvejis yra vaizdo kamerų, teleskopų, mikroskopų bei litografinių sistemų skyra.
Istorija[redaguoti | redaguoti vikitekstą]

Optinių bangų difrakcijos teorijos pagrindą padėjo F. M. Grimaldi (Grimaldi) (1618–1663), sukūręs terminą „difrakcija“, nuo lotynų „diffringere“, „skaidyti į dalis“ bei apibūdino šviesos elgesį žodžiu „diffractio“, kas reiškė „šviesos nuokrypį nuo sklidimo tiesės“ [2][3]. R. Hukas (Hook) (1635–1703), C. Hiuigensas (Huygens) (1629–1695) ir T. Jungas (Young) (1773–1829) taip pat prisidėjo prie difrakcijos teorijos vystymosi, o matematiškai teoriją suformulavo A. J. Frenelis (Fresnel) (1788–1827).
Nedifraguojančios bangos[redaguoti | redaguoti vikitekstą]
Daugiau kaip du amžius Hiuigenso-Frenelio teorija buvo laikoma labai sėkminga teorija, tiksliai aprašanti šviesos sklidimą tiesinėje terpėje. Šios teorijos pagrindas buvo Hiuigenso paskelbti ir Frenelio matematiškai suformuluoti principai, skelbę, kad a) visi bangos fronto paviršiai yra antrinių bangų sferiniai šaltiniai ir b) šviesos laukas visuose būsimuose taškuose yra lemiamas šių sferinių šaltinių šviesos superpozicija.
Nedifraguojančių impulsinių pluoštų laisvoje erdvėje sąvoką į optiką įvedė 1983 m. J. N. Britingemas (Brittingham) paskelbęs [4], kad jis aptiko trimačių, neplintančių, laisvoje bekrūvėje erdvėje sklindančių, klasikinių elektromagnetinių impulsų šeimą, kurie sklinda išilgai tiesės šviesos greičiu (vėliau jie buvo pavadinti židinio bangų modomis, nuo angl. „focus wave modes“). Pati antrinių sferinių šaltinių idėja klasikinės optikos difrakcijos teorijoje savo esmėje slepia teiginį, kad bet kokio impulsinio bangų paketo erdvinis amplitudžių skirstinys turi sklidimo metu išplisti kaip skersinėje, taip ir išilginėje plokštumoje. Iš šių pozicijų Brittingham’o atradimas buvo stulbinantis ir sąlygojo didelį susidomėjimą bei abejones. Tačiau, originalios nedifraguojančios bangos buvo, be abejonės, Maksvelo (Maxwell) lygčių sprendinys ir šis prieštaravimas turėjo būti paaiškintas. Britingemas’as teigė, kad matematinė nedifraguojančių bangų formuluotė a) tenkina homogenines Maksvelo lygtis, b) yra tolydi ir netrūki banga, c) pasižymi trimačio impulso sandara, d) neplinta laike, e) juda šviesos greičiu išilgai tiesės ir f) perneša baigtinį kiekį elektromagnetinio lauko energijos. Šios matematinės formulės nusako trimatį elektromagnetinį darinį, kuris gali būti apibūdintas kaip „šviesos kulka“. Nors paskutinis teiginys, kaip buvo parodyta vėliau [5], buvo neteisingas, darbas pagimdė pačią šviesos kulkų idėją ir sąlygojo kitų uždarų Maksvelo lygčių sprendinių, pasižyminčių panašiomis savybėmis atsiradimą.
Vėliau buvo parodyta, kad bet koks baigtinės energijos bangų lygties sprendinys būtinai turi difraguoti ir plisti erdvėje [6] , tad prieštaravimas su klasikine Hiuigenso-Frenelio teorija buvo panaikintas. Po kiek laiko R. W. Ciolkovskis (Ziolkowski) parodė, kad begalinės energijos židinio bangų modų superpozicija gali sąlygoti baigtinės energijos darinio atsiradimą [7]. Šis rezultatas sąlygojo baigtinės energijos bei uždaros formos bangų ir Maksvelo lygčių sprendinių atsiradimą – „elektromagnetinių kryptingų impulsų vorų“ (angl. “electromagnetic directed-energy pulse trains” (EDEPT)) [8], [9], pliūpsnio impulsų (angl. „splash pulses“), elektromagnetinių raketų [10] ir kt.
Tačiau iki 1987 m., kuomet Durnin’as paskelbė savo darbą apie nedifraguojančius Beselio pluoštus [11], [12], didžioji dalis pastangų suvokti fizikinę mechanizmo esmę buvo iš esmės bevaisės. Tam trukdė teoriniuose darbuose naudojami plokščių bangų skleidiniai, paslepiantys kūginę šio reiškinio esmę. Matematiniu požiūriu lokalizuotas elektromagnetinis laukas yra aprašomas keturmačiu integralu pagal visus įmanomus plokščių bangų laisvės laipsnius. Durnin’o cilindrinių nedifraguojančių bangų idėja sukėlė susidomėjimą ir teoriniuose darbuose buvo pradėti taikyti skleidiniai Beselio funkcijomis. Šis metodas pasirodė efektyvus, ir akustikoje buvo aptiktos “X-bangos” – kitas uždaros formos nedifraguojantis begalinės energijos laukas [13] [14]. Tačiau dėl savo teorinio išvedimo metodo fizikinė reiškinio esmė buvo aiški – skirtingo dažnio bei amplitudžių Beselio pluoštų superpozicija, kurių bangų vektoriai guli ant to paties kūgio. Iš akustikos šios bangos atkeliavo ir į optiką [15].
Nedifraguojančių bangų koncepcija neprieštarauja difrakcijos teorijai, kadangi optikoje yra žinomi pavyzdžiai, kuomet fizikinis procesas pasireiškia ne vien tik destruktyviai, bet ir konstruktyviai. Ryškiausias tokio fizikinio proceso pavyzdys optikoje yra bangų interferencija. Nedifraguojančių bangų fenomenas egzistuoja dėl trapaus balanso tarp konstruktyvios interferencijos ir destruktyvios difrakcijos.
Nedifraguojančių bangų pavyzdžiai[redaguoti | redaguoti vikitekstą]
Elementari nedifraguojanti monochromatinė banga yra plokščia banga – jos amplitudė ir intensyvumas nekinta erdvėje, jai sklindant jokie pokyčiai joje nevyksta, o bangos energija yra begalinė. Plokščią elektromagnetinę bangą aprašo formulė
,
kur E yra bangos poliarizaciją nusakantis vektorius, r – vektorius, jungiantis koordinačių pradžią su nagrinėjamu tašku, o k – bangos vektorius. Baigtinės energijos atitikmuo šiai bangai yra Gauso pluoštas, kuris su baigtinės energijos įgijimu prarado savo isodifrakcines savybes.
Užrašę bangų lygtį cilindrinėje koordinačių sistemoje
gauname kitą elementarų bangų lygties sprendinį – cilindrinę bangą
kur yra m-tos eilės pirmos arba antros rūšies Hankelio (Hankel) funkcija, didelėms r vertėms turinti plokščios bangos asimptotiką , o arti ašies aprašoma kaip , kai m>0 ir , kai m=0. Cilindrinės Hankelio funkcijos gali būti išreikštos per Beselio ir Noimano funkcijas , kurios yra dar vadinamos cilindrinėmis kosinuso ir sinuso funkcijomis. Noimano funkcija ties ašimi įgyja begalines vertes ir naudojama aprašyti begalinės galios šviesą sugeriantį arba spinduliuojantį cilindrinį siūlą. Beselio funkcija naudojama aprašyti situacijas, kuomet šviesa ašyje nėra nei kuriama, nei sugeriama. Kuomet , tokios bangos šaltinis yra begalinis siūlas arba cilindras, o jos bangos frontas atkartos šaltinio simetriją arba vieną iš koordinatinių paviršių. Kuomet , bangos frontas yra kūgis ir atitinka sklindančio išilgai ašies cilindrinio šaltinio spinduliuotę. Stovinti skersinėje plokštumoje banga yra aprašoma Beselio funkcija . Kuomet tokia banga turi judėjimą z ašimi aprašančią dedamąją , gauname klasikinį nedifraguojantį Beselio pluoštą, kuris yra plokščia banga erdvėje moduliuota Beselio funkcija. Šios bangos amplitudė bei intensyvumas taip pat nekinta išilginiame atstume, tačiau, skirtingai nuo plokščios bangos, ji nėra homogeninė skersinėje plokštumoje. Bangą yra aprašoma šia išraiška
kur z yra išilginė koordinatė, r yra skersinė koordinatė. Šios bangos energija yra taip pat begalinė, tačiau baigtinės energijos atitikmuo Beselio ir Gauso pluoštas. Beselio ir Gauso pluoštas, skirtingai nuo Gauso pluošto, išlaiko dalį Beselio pluošto savybių – jis nedifraguoja baigtiniame atstume, vadinamame Beselio zona.
Be minėtų koordinačių sistemų taip pat yra įmanoma sukurti nedifraguojančias bangas apibendrintose cilindrinėse – jos gaunamos iš dvimačių pridėjus z koordinatę – arba apibendrintose sferinėse koordinatėse – jos gaunamos iš dvimačių koordinačių pasukus jas apie vieną iš ašių. Informacijos perdavimui aprašyti yra parankesnės cilindrinės koordinačių sistemos, kadangi cilindro ašis z atitinka informacijos perdavimo kryptį, o skersinėse koordinatėse slypi informacija apie šaltinio arba uždavinio simetriją.
Elipsinio cilindro koordinačių sistemoje skersinės koordinatės u, v siejasi su Dekarto x, y sąryšiu , kur yra koordinatinės elipsės pusašių kvadratų skirtumas. Tokioje koordinačių sistemoje skersinę bangos priklausomybę aprašanti diferencialinė lygtis yra užrašoma
Atskyrę kintamuosius gauname diferencialines lygtis radialinei ir azimutinei priklausomybei
kur . Pirmos lygties sprendinys yra radialinė Matje funkcija, o antros – kampinė Matje funkcija. Kampinės Matje sprendiniai skirstomi į periodinius ir į neperiodinius ir , pastarieji neaprašo periodinių bangų sklidimą. Periodiniai azimutinės lygties sprendiniai yra dar vadinami elipsiniais kosinusu ir sinusu ir atitinka lyginį (e) arba nelyginį (o) radialinės Matje lygties sprendinį. Radialinės Matje lygties sprendiniai yra Beselio, Noimano ir Hankelio funkcijų apskritiminio cilindro koordinatėse atitikmenys ir yra žymimos lyginėms azimutinėms funkcijoms ir – nelyginėms. Tuo būdu, nedifraguojanti sklindanti banga šiose koordinatėse yra užrašoma
Difrakcijos mechanizmas[redaguoti | redaguoti vikitekstą]
Klasikinis difrakcijos paaiškinimas yra grindžiamas interferencija. Kuomet dvi vienodo dažnio ir vienodos sklidimo krypties bangos susitinka, jų amplitudės susideda ir suminė banga turi arba didesnę, arba mažesnę amplitudę, priklausomai nuo fazių skirtumo tarp pradinių bangų. Difrakcija nuo neskaidraus objekto gali būti įsivaizduota kaip skirtingų bangos dalių interferencija už difrakciją sąlygojusio objekto. Intensyvumo skirstinys susidaręs dėl šios interferencijos priklauso nuo bangos ilgio, kas sąlygoja vaivorykštės spalvų atsiradimą nuo CD disko difragavusioje šviesoje. Konkrečios spalvos difraguoja konkrečiais erdviniais kampais dėl to, kad tik ta kryptimi visos antrinės bangos interferuoja konstruktyviai, tuo tarpu kitomis kryptimis vyksta destruktyvi interferencija. Didžioji dalis difrakcijos reiškinių gali būti suvokta pasitelkus paprastas sąvokas.
Paprasčiausia eksperimentinė situacija, kuomet yra stebima difrakcija, sutinkama kuomet ekrane padaromas plyšys, kurio matmenuo yra mažesnis už eksperimente naudojamą bangos ilgį. Po to, kai banga nukeliauja pro plyšį, susidaro koncentrinių apskritimų sistema, lyg plyšio centre būtų taškinis bangų šaltinis. Ši koncentrinių apskritimų sistema yra difragavusios bangos skirstinys.
Jei mes padarytume ekrane antrą tokį pat siaurą plyšį pakankamai arti pirmojo, tuomet dviejų taškinių bangų šaltinių kuriamos bangos tarpusavyje interferuotų. Jei įsivaizduotume vandens paviršiuje sklindančių bangų interferencija, tuomet vandens paviršiuje būtų taškai, kuriuose atsidurtų atskirų bangų vienodi arba skirtingi ekstremumai. Kuomet ekstremumai būtų vienodi (abu maksimumai arba minimumai), mes stebėtume bendros bangos sustiprėjimą, priešingu atveju vandens lygis laikui bėgant nesikeistų.
Šviesai sutikus daug vienodais atstumais vienas nuo kito nutolusių plyšių, kiekvienas plyšys sukuria taškinį bangos šaltinį. Kiekvieno tokio šaltinio kuriama banga interferuotų su kitų taškinių šaltinių kuriamomis bangomis ir atsirastų erdvėje kryptis, ties kuriomis visų taškinių šaltinių ekstremumai sutaptų, o ties kitomis nesutaptų. Būtent šio principu veikia difrakcinė gardelė.
Platesnius plyšius taip pat galime įsivaizduoti, kaip šalia vienas kito esančius nepriklausomus taškinius plyšius, kiekvienas iš kurių kuria savo radialinę bangelę. Šis principas yra žinomas kaip Hiuigenso-Frenelio principas: kiekvienas sklindančios bangos fronto taškas gali būti įsivaizduojamas kaip antrinės bangelės taškinis šaltinis, o naujasis bangos frontas yra visų šių taškinių šaltinių bendro bangos lauko vienodos fazės paviršius.
Dalelių difrakcija[redaguoti | redaguoti vikitekstą]
Vienas esminių kvantinės mechanikos teiginių yra de Broilio hipotezė apie dvilypę dalelių prigimtį – kiekvienai dalelei galima priskirti banginį procesą. Dėl šios priežasties įvairios dalelės gali interferuoti ir difraguoti. Eksperimentų metų užfiksuota elektronų ir neutronų difrakcija buvo vienas svariausių argumentų pagrindžiančių kvantinę mechaniką. Su dalele siejamas banginis procesas gali būti apibūdintas bangos ilgio sąvoka, kuris pabrėžiant, kad kalbama apie dalelę yra vadinamas de Broilio bangos ilgiu
kur h yra Planko konstanta ir p yra dalelės judesio kiekis (masė × lėtai judančios dalelės greitis). Makroskopiniams objektams, šis bangos ilgis yra toks mažas, kad bangos ilgio sąvoka netenka prasmės. Natrio atomas, lekiantis 3000 m/s greičiu turėtų de Broilio bangos ilgį apytiksliai lygu 5 pikometrams.
Dėl tos priežasties, kad šis bangos ilgis net mažiausiems makroskopiniams objektams yra ypatingai mažas, medžiagos bangų difrakcija yra stebima tik smulkioms dalelėms, tokioms kaip elektronai, neutronai, atomai ir smulkio molekulės ir įvairios elementarios dalėlės. Ypatingai trumpo medžiagos bangų ilgiai daro jas puikiu įrankiu kietų kūnų atomų kristalinių gardelių bei stambių proteinų molekulių tyrimams.
Nesenai buvo stebėta ir stambesnių molekulių difrakcija,[16] bei yra kalbama apie virusų difrakciją. Dėl žymiai didesnių virusų matmenų lyginant juos su elektronu, tam, kad jie difraguotų pereidami per plyšį, jie turi judėti labai mažais greičiais – tik tuomet jų de Broilio bangų ilgiai taps didesni.
Brego difrakcija[redaguoti | redaguoti vikitekstą]

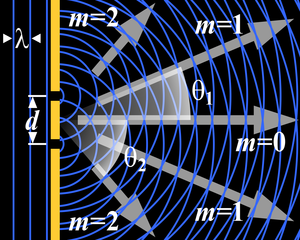
Difrakcija nuo trimatės periodinės sandaros, tokios kaip atomai kristalų gardelėse, yra vadinama Brego difrakcija. Šios difrakcijos metu vykstantys procesai yra panašus į bangų difrakcija nuo difrakcinės gardelės. Brego difrakcija yra aiškinama konstruktyvia bangų atsispindėjusių nuo skirtingų kristalinės gardelės plokštumų, interferencija.
Konstruktyvios interferencijos sąlygos yra apibrėžiamos sąryšiu, vadinamu Brego dėsniu:
kur
- λ yra bangos ilgis,
- d yra atstumas tarp kristalinės gardelės plokštumų,
- θ difragavusios bangos kampas.
- ir m yra sveikas skaičius, vadinamas difragavusio spindulio eile.
Brego difrakcija yra stebima apšvietus kristalinę medžiaga arba labai trumpų bangos ilgių šviesa (Rentgeno spinduliai) arba medžiagos bangomis (neutronai), kadangi šių banginių procesų bangų ilgiai yra tos pačios eilės kaip ir atstumai tarp atomų. Difrakcinis skirstinys slepia informaciją apie atstumus d tarp skirtingų kristalografinių plokštumų, taip įgalindamas nustatyti medžiagos kristalinės gardelės sandarą.
Nuorodos[redaguoti | redaguoti vikitekstą]
- ↑ Dietrich Zawischa. „Optical effects on spider webs“. Nuoroda tikrinta 2007-09-21.
- ↑ Jean Louis Aubert (1760). Memoires pour l'histoire des sciences et des beaux arts. Paris: Impr. de S. A. S.; Chez E. Ganeau. p. 149.
- ↑ Sir David Brewster (1831). A Treatise on Optics. London: Longman, Rees, Orme, Brown & Green and John Taylor. p. 95.
- ↑ Brittingham, J.N. (1983). „Focus wave modes in homogeneous Maxwell equations: Transverse electric mode“. J. Appl. Phys. 54: 1179.
- ↑ Wu, T. T.; R. W. P. King (1984). „Comments on focus wave modes in homogeneous. Maxwell equations: Transverse electric mode“. J. Appl. Phys. 56: 2587.
- ↑ Wu, T. T.; H. Lehmann (1985). „Spreading of electromagnetic pulses“. J. Appl. Phys. 58: 2064.
- ↑ Ziolkowski, R. W. (1985). „Exact solutions of the wave equation with complex source locations“. J. Math. Phys. 26: 861.
- ↑ Ziolkowski, R. W. (1989). „Localized transmission of electromagnetic energy“. Phys. Rev. A. 39: 2005.
- ↑ Ziolkowski, R. W. (1991). „Localized wave physics and engineering“. Phys. Rev. A. 44: 3960.
- ↑ Wu, T. T. (1985). „Electromagnetic missile“. J. Appl. Phys. 57: 2370.
- ↑ Durnin, J.; J. J. Miceli, J. M. Eberly (1987). „Diffraction-Free Beams“. Phys. Rev. Lett. 58: 1499.
- ↑ Durnin, J. (1987). „Exact solutions for nondiffracting beams. I. The scalar theory“. J. Opt. Soc. Am. A. 4: 651.
- ↑ Lu, J.-Y.; J. G. Greenleaf (1992). „Nondiffracting X-waves: Exact solutions to free-space scalar wave equation and their finite aperture realizations“. IEEE Trans. Ultrason. Ferroelectr. Freq. Control. 39: 19.
- ↑ Lu, J.-Y.; J. G. Greenleaf (1994). „Biomedical ultrasound beam forming“. Ultrasound in Mol. & Biol. 20: 403.
- ↑ Salo, J.; J. Fagerholm, A. T. Friberg, and M. M. Salomaa (2000). „Unified description of nondiffracting X and Y waves“. Phys. Rev. 62: 4260.
{{cite journal}}: CS1 priežiūra: multiple names: authors list (link) - ↑ Brezger, B.; Hackermüller, L.; Uttenthaler, S.; Petschinka, J.; Arndt, M.; Zeilinger, A. (2002 m. vasario mėn.). „Matter-Wave Interferometer for Large Molecules“ (PDF). Physical Review Letters. 88 (10): 100404. doi:10.1103/PhysRevLett.88.100404. Suarchyvuotas originalas (reprint) 2007-08-13. Nuoroda tikrinta 2007-04-30.
{{cite journal}}: CS1 priežiūra: multiple names: authors list (link)



![{\displaystyle E\left(r,\phi ,z,t\right)=E_{0}H_{m}^{\left(1,2\right)}\left(k_{r}r\right)\exp \left[\mathrm {i} \left(k_{z}z-\omega t\right)\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/4319713e011c0b22067c4a45561f2bdba5c3c6ed)













![{\displaystyle \left[{\frac {\partial ^{2}}{\partial u^{2}}}+{\frac {\partial ^{2}}{\partial \upsilon ^{2}}}+{\frac {\alpha ^{2}}{2}}\left(\cosh 2u-\cos 2\upsilon \right)\right]U_{r}\left(u,\upsilon \right)=0.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/a9df3dc567da594fc3ddfad28a04c5844e78bc06)

![{\displaystyle \left[{\frac {\partial ^{2}}{\partial u^{2}}}-\left(a-2q\cosh 2u\right)\right]R\left(u\right)=0,\quad \left[{\frac {\partial ^{2}}{\partial \upsilon ^{2}}}-\left(a-2q\cos 2\upsilon \right)\right]\Theta \left(\upsilon \right)=0,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/5c432399ae0b71c330e62b5ebc77056ef89de948)






![{\displaystyle E\left(u,\upsilon ,z,t\right)=E_{0}Je_{m}\left(u;q\right)ce_{m}\left(\upsilon ;q\right)\exp \left[\mathrm {i} \left(\pm k_{z}z-\omega t\right)\right],}](https://wikimedia.org/api/rest_v1/media/math/render/svg/23026b636da8045dbe7fe6486a2be2d20583d0e4)
![{\displaystyle E\left(u,\upsilon ,z,t\right)=E_{0}Jo_{m}\left(u;q\right)se_{m}\left(\upsilon ;q\right)\exp \left[\mathrm {i} \left(\pm k_{z}z-\omega t\right)\right].}](https://wikimedia.org/api/rest_v1/media/math/render/svg/91dd831e989eed7b7aa46ef877bc0b397371e0b1)

