Beselio funkcija

Beselio funkcijos apibūdina radialinę apskritosios membranos virpesių dalį.

Beselio funkcijos – kanoniniai Beselio diferencialinės lygties

$x^{2}{\frac {d^{2}y}{dx^{2}}}+x{\frac {dy}{dx}}+(x^{2}-\alpha ^{2})y=0$

sprendiniai bet kokiai realiai arba kompleksinei parametro $\alpha$ vertei. Labiausiai paplitę ir svarbūs daliniai atvejai, kai $\alpha$ yra sveikas skaičius n. Tada parametras $\alpha$ yra vadinamas Beselio funkcijos eile.

Beselio funkcijos pirmą kartą apibrėžtos matematiko Danielio Bernulio, o apibendrintos Frydricho Beselio.

Beselio funkcija taikymuose

Beselio diferencialinė lygtis atsiranda matematinėje fizikoje, kuomet Laplaso lygtyje arba Helmholco lygtyje yra atskiriami kintamieji, lygtis užrašius cilindrinėje arba sferinėje koordinačių sistemose. Dėl šios priežasties Beselio funkcijos yra ypač svarbios daugelyje bangų fizikos uždavinių. Spręsdami cilindrinės simetrijos uždavinius, susiduriame su su lyginės (α = n) eilės Beselio funkcijomis, tuo tarpu sferinėse koordinatėse sutinkamos pusinių (α = n + ½) eilių Beselio funkcijos. Pavyzdžiui

• Elektromagnetinė banga cilindriniame bangolaidyje.
• šilumos pernaša cilindriniame objekte.
• Nuosavų virpesių modos plonoje apskritiminėje membranoje (būgno plėvelė).
• Mie sklaidos uždaviniai.

Apibrėžimai

Kadangi Beselio funkcijos yra antros eilės diferencialinės lygties sprendiniai, egzistuoja dvi tarpusavyje tiesiškai nepriklausomos funkcijos. Priklausomai nuo aplinkybių, sprendinių poros yra skirtingai apibrėžiamos.

Pirmos rūšies Beselio funkcijos : J_α

Pirmos rūšies Beselio funkcijos, žymimos simboliu $J_{\alpha }(x)$, yra Beselio diferencialinės lygties sprendiniai, turintys baigtinę vertę koordinačių pradžios taške ($x=0$) neneigiamoms sveiko skaičiaus $\alpha$ vertėms, ir diverguoja, kai koordinatė $x$ artėja prie nulio neigiamoms ir nelygioms sveikam skaičiui parametro $\alpha$ vertėms. Sprendinio tipas (t. y. sveikas skaičius arba nesveikas) funkcijos $J_{\alpha }(x)$ vertės yra apibrėžiamos žemiau. Šios funkcijos Teiloro eilutė taško $x=0$ aplinkoje užrašoma taip:

$J_{\alpha }(x)=\sum _{m=0}^{\infty }{\frac {(-1)^{m}}{m!\Gamma (m+\alpha +1)}}{\left({\frac {x}{2}}\right)}^{2m+\alpha }$

kur $\Gamma (z)$ yra Gama funkcija, faktorialo funkcijos apibendrinimas nesveikiems skaičiams. Beselio funkcijos grafikai atrodo panašiai į osciliuojančias sinuso ir kosinuso funkcijas, kurios slopsta proporcingai funkcijai 1/√x (taip pat žr. jų asimptotines formas žemiau) tolstant nuo koordinačių centro. Nors Beselio funkcijos šaknys, griežtai tariant, nėra periodinės, asimptotikoje jos sutampa su sinuso ir kosinuso funkcijų šaknimis. (Teiloro eilutės pavidalas byloja apie tai, kad $-J_{1}(x)$ yra funkcijos $J_{0}(x)$ išvestinė, analogiškai kaip $-\sin(x)$ yra funkcijos $\cos(x)$ išvestinė; bendru atveju, funkcijos $J_{n}(x)$ išvestinė gali būti išreikšta kaip funkcijų $J_{n\pm 1}(x)$ suma.)

Pirmos rūšies Beselio funkcijų J_α(x) grafikai sveikoms eilėms α=0,1,2.

Nesveikoms α vertėms, funkcijos $J_{\alpha }(x)$ ir $J_{-\alpha }(x)$ yra tiesiškai nepriklausomos, tuo būdu budamos vienintelė diferencialinės lygties sprendinių pora. Iš kitos pusės, sveikoms eilėms $\alpha$, galioja sekantis sąryšis:

$J_{-n}(x)=(-1)^{n}J_{n}(x).\,$

Tai reiškia, kad du sprendiniai nėra tiesiškai nepriklausomi. Šiuo atveju, yra įvedama antros rūšies Beselio funkcija Y_α.

Beselio integralai

Yra įmanoma apibrėžti Beselio funkcija sveikoms eilėms $n$, kaip integralą:

$J_{n}(x)={\frac {1}{\pi }}\int _{0}^{\pi }\cos(n\tau -x\sin \tau )\,\mathrm {d} \tau .$

Tokiame pavidale šią funkciją pirmą kartą užrašė Beselis ir iš šio apibrėžimo buvo išvestos pirmosios funkcijos savybės.

Egzistuoja ir kitas integralinis atvaizdavimas:

$J_{n}(x)={\frac {1}{2\pi }}\int _{-\pi }^{\pi }e^{-\mathrm {i} \,(n\tau -x\sin \tau )}\,\mathrm {d} \tau .$

Saryšis su Lagero polinomais

Egzistuoja formulė, siejanti Beselio funkcija su Lagero polinomais bei laisvai pasirinktu parametru $t$

${\frac {J_{\alpha }(x)}{\left({\frac {x}{2}}\right)^{\alpha }}}={\frac {e^{-t}}{\Gamma (\alpha +1)}}\sum _{i=0}{\frac {L_{i}^{(\alpha )}\left({\frac {x^{2}}{4t}}\right)}{i+\alpha \choose i}}{\frac {t^{i}}{i!}}.$

Antros rūšies Beselio funkcijos Y_α

Antros rūšies Beselio funkcija yra žymima Y_α(x) ir yra sprendinių pora, užbaigianti funkcijų šeimą. Šios funkcijos įgija begalinės vertės ties koordinačių pradžia (x = 0).

Antros rūšies Beselio funkcijų Y_α(x) grafikai sveikoms eilėms α=0,1,2.

Y_α(x) yra kartais vadinama Noimano funkcija ir tekstuose žymima N_α(x). Nesveikoms eilėms α, funkcija siejasi su pirmos rūšies funkcija J_α(x) sąryšiu:

$Y_{\alpha }(x)={\frac {J_{\alpha }(x)\cos(\alpha \pi )-J_{-\alpha }(x)}{\sin(\alpha \pi )}}.$

Kuomet eilė n yra sveikas skaičius, funkcija yra apibrėžiama radus nesveiko skaičiaus α ribą, kuomet jis artėja prie sveiko skaičiaus 'n':

$Y_{n}(x)=\lim _{\alpha \to n}Y_{\alpha }(x),$

Riba yra apskaičiuojama ir jos integralinis atvaizdavimas yra

$Y_{n}(x)={\frac {1}{\pi }}\int _{0}^{\pi }\sin(x\sin \theta -n\theta )d\theta -{\frac {1}{\pi }}\int _{0}^{\infty }\left[e^{nt}+(-1)^{n}e^{-nt}\right]e^{-x\sinh t}dt.$

Tais atvejais, kai α yra nesveikas skaičius, Y_α(x) apibrėžimas nėra būtinas, kadangi ji yra priklausoma nuo pirmos rūšies funkcijos. Iš kitos pusės, kuomet α yra sveikas skaičius, Y_α(x) yra antras tiesiškai nepriklausomas Beselio diferencialinės lygties sprendinys, todėl ir šiai funkcijai galioja sąryšis:

$Y_{-n}(x)=(-1)^{n}Y_{n}(x).\,$

Hankelio funkcijos: H_α

Kita svarbi galimybė apibrėžti dvi nepriklausomas Beselio diferencialinės lygties sprendinių šeimas yra Hankelio funkcijos H_α⁽¹⁾(x) ir H_α⁽²⁾(x), apibrėžiamos kaip:

$H_{\alpha }^{(1)}(x)=J_{\alpha }(x)+iY_{\alpha }(x)$

$H_{\alpha }^{(2)}(x)=J_{\alpha }(x)-iY_{\alpha }(x)$

kur i yra menamas vienetas. Šios tiesinės kombinacijos taip pat yra vadinamos trečios rūšies Beselio funkcijomis; jos yra du tiesiškai nepriklausomi Beselio diferencialinės lygties sprendiniai. Hankelio pirmos ir antros rūšių funkcijos fizikoje yra naudojamos aprašyti nuo koordinačių pradžios tolstančias ir artėjančias cilindrines bangas, atitinkamai, kurios gaunamos išsprendus bangų lygtį.

Su prieš tai paminėto sąryšio pagalba, jos gali būti išreikštos:

$H_{\alpha }^{(1)}(x)={\frac {J_{-\alpha }(x)-e^{-\alpha \pi i}J_{\alpha }(x)}{i\sin(\alpha \pi )}}$

$H_{\alpha }^{(2)}(x)={\frac {J_{-\alpha }(x)-e^{\alpha \pi i}J_{\alpha }(x)}{-i\sin(\alpha \pi )}}$

jei α yra sveikas skaičius, yra būtina skaičiuoti ribą. Sekantys sąryšiai yra teisingi nepriklausomai nuo to, ar α yra sveikas, ar ne:

$H_{-\alpha }^{(1)}(x)=e^{\alpha \pi i}H_{\alpha }^{(1)}(x)$

$H_{-\alpha }^{(2)}(x)=e^{-\alpha \pi i}H_{\alpha }^{(2)}(x)$

Modifikuotos Beselio funkcijos : I_α, K_α

Beselio funkcijų apibrėžimai yra teisingi ir kompleksinėms argumento vertėms, kas reiškia, jog įmanoma apibrėžti funkcijas nuo menamo argumento x. Šiuo atveju, Beselio diferencialinės lygties sprendiniai yra vadinami pirmos ir antros rūšies modifikuotomis Beselio funkcijomis (kartais hiperbolinėmis Beselio funkcijomis):

$I_{\alpha }(x)=i^{-\alpha }J_{\alpha }(ix)\!$

$K_{\alpha }(x)={\frac {\pi }{2}}{\frac {I_{-\alpha }(x)-I_{\alpha }(x)}{\sin(\alpha \pi )}}={\frac {\pi }{2}}i^{\alpha +1}H_{\alpha }^{(1)}(ix)\!$

Šios funkcijos įgyja realias vertes realioms argumento x vertėms. Funkcijos I_α(x) skleidinys eilute todėl yra panašus į funkcijos J_α(x) skleidimą eilute, bet be besikeičiančio (−1)^m daugiklio.

I_α(x) ir K_α(x) yra nepriklausomų funkcijų pora, atitinkanti modifikuotą Beselio diferencialinę lygtį:

$x^{2}{\frac {d^{2}y}{dx^{2}}}+x{\frac {dy}{dx}}-(x^{2}+\alpha ^{2})y=0.$

Skirtingai nuo paprastų Beselio funkcijų, kurios yra osciliuojančios funkcijos, I_α ir K_α yra eksponentiškai augančios ir slopstančios funkcijos, atitinkamai. Kaip ir paprastoji Beselio funkcija J_α, funkcija I_α artėja prie nulio, kai x = 0 ir α > 0, bei yra baigtinė, kai x = 0 ir α = 0. Analogiškai, K_α diverguoja ties x = 0.

Pirmos rūšies modifikuotų Beselio funkcijų Iα(x) grafikai sveikoms eilėms α=0,1,2,3.

Antros rūšies modifikuotų Beselio funkcijų Kα(x) grafikai sveikoms eilėms α=0,1,2,3.

Sferinės Beselio funkcijos : j _n, y _n

Pirmos rūšies sferinės Beselio funkcijos, j_n(x), kai n = 0, 1, 2

Antros rūšies sferinės Beselio funkcijos, y_n(x), kai n = 0, 1, 2

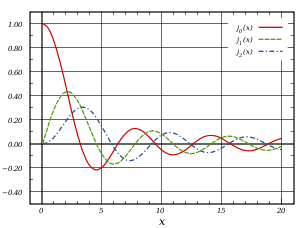
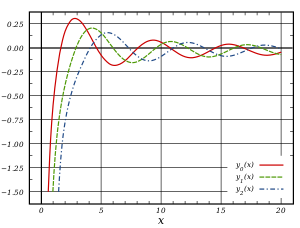
Sprendžiant bangų lygtį sferinėse koordinatėse kintamųjų atskyrimo metodu, radialinę priklausomybę aprašanti lygtis yra:

$x^{2}{\frac {d^{2}y}{dx^{2}}}+2x{\frac {dy}{dx}}+[x^{2}-n(n+1)]y=0.$

Du tiesiškai nepriklausomi šios lygties sprendiniai yra vadinami sferinėmis Beselio funkcijomis j_n ir y_n, jos siejasi su paprastomis BEselio funkcijomis J_n ir Y_n sąryšiu:

$j_{n}(x)={\sqrt {\frac {\pi }{2x}}}J_{n+1/2}(x),$

$y_{n}(x)={\sqrt {\frac {\pi }{2x}}}Y_{n+1/2}(x)=(-1)^{n+1}{\sqrt {\frac {\pi }{2x}}}J_{-n-1/2}(x).<math>y_{n}$ taip pat žymima $n_{n}$ arba η_n; kai kurie autoriai vadina šias funkcijas sferinėmis Neumano funkcijomis.

Sferinės Beselio funkcijos gali būti užrašomos:

$j_{n}(x)=(-x)^{n}\left({\frac {1}{x}}{\frac {d}{dx}}\right)^{n}\,{\frac {\sin x}{x}},$

$y_{n}(x)=-(-x)^{n}\left({\frac {1}{x}}{\frac {d}{dx}}\right)^{n}\,{\frac {\cos x}{x}}.$

Pirmoji sferinė Beselio funkcija $j_{0}(x)$ yra taip pat žinoma kaip nenormuota sinc funkcija. Kelios pirmosios sferinės Beselio funkcijos yra:

$j_{0}(x)={\frac {\sin x}{x}}$

$j_{1}(x)={\frac {\sin x}{x^{2}}}-{\frac {\cos x}{x}}$

$j_{2}(x)=\left({\frac {3}{x^{2}}}-1\right){\frac {\sin x}{x}}-{\frac {3\cos x}{x^{2}}},$

ir

$y_{0}(x)=-j_{-1}(x)=-\,{\frac {\cos x}{x}}$

$y_{1}(x)=j_{-2}(x)=-\,{\frac {\cos x}{x^{2}}}-{\frac {\sin x}{x}}$

$y_{2}(x)=-j_{-3}(x)=\left(-\,{\frac {3}{x^{2}}}+1\right){\frac {\cos x}{x}}-{\frac {3\sin x}{x^{2}}}.$

Taip pat egzistuoja sferiniai Hankelio funkcijų analogai:

$h_{n}^{(1)}(x)=j_{n}(x)+iy_{n}(x)$

$h_{n}^{(2)}(x)=j_{n}(x)-iy_{n}(x).$

Egzistuoja paprasti glausti sąryšiai tarp pusinės eilės Beselio funkcijų ir trigonometrinių funkcijų, dėl šios priežasties tokie pat sąryšiai egzistuoja ir tarp pusinės eilės Beselio funkcijų ir sveikos eilės sferinių Beselio funkcijų. Teigiamiems sveikiems skaičiams n galioja:

$h_{n}^{(1)}(x)=(-i)^{n+1}{\frac {e^{ix}}{x}}\sum _{m=0}^{n}{\frac {i^{m}}{m!(2x)^{m}}}{\frac {(n+m)!}{(n-m)!}}$

ir $h_{n}^{(2)}$ yra kompleksiškai jungtinis dydis (realioms $x$ vertėms). Iš čia seka, kaip pavyzdys, kad $j_{0}(x)=\sin(x)/x$ ir $y_{0}(x)=-\cos(x)/x$, ir t. t.

Asimptotika

Beselio funkcijos turi sekančią asimptotines formas neneigiamiems α. Mažoms argumento vertėms $0<x\ll {\sqrt {\alpha +1}}$, gauname:

$J_{\alpha }(x)\rightarrow {\frac {1}{\Gamma (\alpha +1)}}\left({\frac {x}{2}}\right)^{\alpha }$

$Y_{\alpha }(x)\rightarrow \left\{{\begin{matrix}{\frac {2}{\pi }}\left[\ln(x/2)+\gamma \right]&{\mbox{if }}\alpha =0\\\\-{\frac {\Gamma (\alpha )}{\pi }}\left({\frac {2}{x}}\right)^{\alpha }&{\mbox{if }}\alpha >0\end{matrix}}\right.$

kur $\gamma$ yra Oilerio-Maskeronio konstanta (0.5772…), o $\Gamma$ pažymi gama funkciją. Dideliems argumentams $x\gg |\alpha ^{2}-1/4|$, funkcijos tampa:

$J_{\alpha }(x)\rightarrow {\sqrt {\frac {2}{\pi x}}}\cos \left(x-{\frac {\alpha \pi }{2}}-{\frac {\pi }{4}}\right)$

$Y_{\alpha }(x)\rightarrow {\sqrt {\frac {2}{\pi x}}}\sin \left(x-{\frac {\alpha \pi }{2}}-{\frac {\pi }{4}}\right).$

(Kai α=1/2 šios formulės yra tikslios; žr. sferinių Beselio funkcijų skyrelį.) Asimptotinės formos kitiems Beselio funkcijų tipams seka tiesiai iš aukščiau užrašytų sąryšių. Pavyzdžiui, dideliems $x\gg |\alpha ^{2}-1/4|$, modifikuotos Beselio funkcijos užsirašo:

$I_{\alpha }(x)\rightarrow {\frac {1}{\sqrt {2\pi x}}}e^{x},$

$K_{\alpha }(x)\rightarrow {\sqrt {\frac {\pi }{2x}}}e^{-x}.$

kuomet mažoms argumento vertėms $0<x\ll {\sqrt {\alpha +1}}$, jos tampa:

$I_{\alpha }(x)\rightarrow {\frac {1}{\Gamma (\alpha +1)}}\left({\frac {x}{2}}\right)^{\alpha }$

$K_{\alpha }(x)\rightarrow \left\{{\begin{matrix}-\ln(x/2)-\gamma &{\mbox{if }}\alpha =0\\\\{\frac {\Gamma (\alpha )}{2}}\left({\frac {2}{x}}\right)^{\alpha }&{\mbox{if }}\alpha >0.\end{matrix}}\right.$

Taip pat skaitykite

• Gauso funkcija
• Beselio pluoštas