Hiugenso ir Frenelio principas
| |
Šiam straipsniui ar jo daliai trūksta išnašų į patikimus šaltinius. Jūs galite padėti Vikipedijai pridėdami tinkamas išnašas su šaltiniais. |

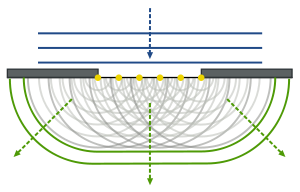
Hiugenso ir Frenelio principas (pavadintas pagal olandų fiziką Christianą Hiugensą ir prancūzų fiziką Augustiną Žan Frenelį) – fizikinis principas, taikomas bangų sklidimo uždavinių analizėje. Jis teigia, kad kiekvienas sklindančios bangos paviršiaus taškas yra antrinių koherentinių bangų voros šaltinis. Besiplečianti banga šioje interpretacijoje gali būti įsivaizduota kaip visų antrinių bangų, sklindančių iš ankstesnių taškų, interferencija.
Pavyzdžiui, jei du kambariai yra sujungti praėjimu ir viename iš kambarių sukuriamas garsas nuo praėjimo nutolusiame kampe, asmuo, esantis antrame kambaryje, girdės šį garsą, lyg jis sklistų iš praėjimo. Kol nagrinėjamas garsas antrame kambaryje, jo šaltinis yra oro virpesiai praėjime tarp kambarių. Panašiu būdu vyksta ir šviesos bangų difrakcija, kuomet šviesa sutinka kliūtį, tačiau tai sunkiai pastebima kasdienybėje dėl trumpų regimos šviesos bangos ilgių
Hiugenso ir Frenelio principas formaliai seka iš kvantinės elektrodinamikos fundamentinių postulatų, teigiančių, kad kiekvieno objekto banginė funkcija sklinda visais įmanomais keliais iš šaltinio į nagrinėjamą tašką. Tokiu būdu šis principas yra visų kontūrinio integralų, apibrėžiančių objekto banginės funkcijos amplitudę ir fazę interferencijos (sudėties) pasekmė bei apibrėžia tikimybę aptikti objektą (tarkim fotoną) nagrinėjamame taške. Ne tik šviesos kvantai (fotonai), bei ir elektronai, neutronai, protonai, atomai, molekulės bei kiti nepaminėti objektai paklūsta šiam paprastam principui.
Difrakcija pro plyšį[redaguoti | redaguoti vikitekstą]
Tegu banga, sklindanti iš taškinio šaltinio turi amplitudę taške r, tuomet amplitudė yra bangų lygties dažnių erdvėje sprendinys
kur yra trimatė Dirako delta funkcija. Delta funkcija turi tik radialinę priklausomybę, todėl Laplaso operatorius (skaliarinis Laplasianas) sferinėse koordinatėse gali būti supaprastintas iki
Tiesiogiai įstatę, galime įsitikinti, kad šios lygties sprendinys yra skaliarinė Gryno funkcija, kuri sferinėse koordinatėse (bei naudojant "fizikinę" laikinę priklausomybę ) užrašoma taip:
Šis sprendinys teigia, kad delta funkcijos šaltinis yra koordinačių sistemos pradžioje. Kuomet šaltinio padėtis yra taškas, į kurį iš koordinačių sistemos pradžios eina vektorius , o nagrinėjamas bangos taškas yra apibrėžiamas vektoriumi , tuomet mes galime užrašyti skaliarinę Gryno funkcija taip
Tokiu būdu, jei elektrinis laukas, Einc(x,y) krenta į plyšį, elektrinis laukas už plyšio yra surandamas iš sekančio paviršinio integralo:
kur šaltinio taškas plyšyje yra
Tolimoje srityje (tolimasis laukas), kuomet iš plyšio sklindantis spinduliai yra apytiksliai lygiagretūs, Gryno funkcija
gali būti supaprastintai užrašyta kaip
Bangos amplitudės išraiška tolimajame lauke (arba Frauenhoferio difrakcijos srityje) tampa
Kadangi
ir
bangos lauko toliamajame lauke išraiška galutinai užrašoma kaip
Tolimesnis išraiškos supaprastinimas gali būti pasiektas pakeitus koordinačių sistema. Tarkim,
ir
Gauname, kad Frauenhoferio difrakcijos metu, plokščią plyšį apšvietusi šviesa, už plyšio yra aprašoma integralu, esančiu kritusios šviesos Furjė atvaizdu.
Tokiu būdu, toli nuo plyšio, pro plyšį praėjusios šviesos laukas yra erdvinis elektrinio lauko plyšyje Furjė atvaizdas. Hiugenso principas pritaikytas difrakcijai pro plyšį teigia, kad tolimasis bangos laukas neša savyje informaciją apie jį sukūrusį plyšį.


















