Trikampis
 Kitos reikšmės – Trikampis (reikšmės).
Kitos reikšmės – Trikampis (reikšmės).

Trikampis – paprasčiausias daugiakampis, turintis tris viršūnes ir tris jas jungiančias kraštines. Visų trikampio vidinių kampų suma lygi 180 laipsnių.
Euklido geometrijoje bet kokie trys ne vienoje linijoje esantys taškai nusako unikalų trikampį ir unikalią plokštumą
Trikampio perimetras apskaičiuojamas pagal formulę P = a+b+c
Savybės
- Bet kurio trikampio visų kampų suma yra 180°.
- Bet kurių dviejų kraštinių suma yra didesnė už trečiosios kraštinės ilgį.
- Bet kurį trikampį galima apibrėžti apskritimu.
- Apibrėžtinio apskritimo centras yra to trikampio kraštinių vidurio statmenų susikirtimo taškas.
- Įbrėžto apskritimo centras yra pusiaukampinių susikirtimo taške.
- Trikampio svorio centras yra pusiaukraštinių susikirtimo taške.
- Trikampio nelygybė: atstumas tarp dviejų taškų ne didesnis už sumą nuo tų taškų iki bet kurio trečio taško.[1]
- Trikampio priekampis (kampas, gretutinis trikampio vidaus kampui) yra didesnis už kiekvieną jam negretutinį vidaus kampą.[2]
Trikampių panašumo ir lygumo požymiai
Trikampiai yra lygūs, kai vieno iš trikampių atitinkamos kraštinės ir kampai yra lygūs kito trikampio kraštinėms ir kampams.[3] Trikampio lygumo požymiai dažnai yra taikomi sprendžiant brėžimo uždavinius, kur galima naudotis tik skriestuvu ir liniuote.[4] Yra išskiriami šie lygumo požymiai:[5]
- Pagal dvi kraštines ir kampą tarp jų
- Pagal kraštinę ir prie jos esančius kampus
- Pagal tris kraštines
Trikampių panašumo požymiai:
- Pagal du kampus
- Pagal dvi kraštines ir kampą tarp jų
- Pagal tris kraštines
Panašiųjų trikampių perimetrų santykis lygus panašumo koeficientui , o jų plotų santykis - panašumo koeficiento kvadratui .[6]
Trikampių rūšys pagal kraštines
Pagal kraštines trikampiai skirstomi į tris rūšis: įvairiakraščius, lygiašonius ir lygiakraščius.
Įvairiakraštis trikampis – trikampis, kurio visos kraštinės skirtingo ilgio.
Lygiašonis trikampis – trikampis, kurio dvi kraštinės tokio pat ilgio. Jos vadinamos šoninėmis kraštinėmis, o trečioji – pagrindu. Lygiašonio trikampio kampai prie pagrindo lygūs. Lygiašonio trikampio aukštinė, pusiaukampinė ir pusiaukraštinė, nubrėžtos į pagrindą sutampa.
Lygiakraštis trikampis – trikampis, kurio visos kraštinės lygios. Visi lygiakraščio trikampio kampai taip pat lygūs.
Žinant lygiakraščio trikampio kraštinės ilgį a, jo plotas randamas pagal formulę
-
Įvairiakraštis trikampis
-
Lygiašonis trikampis
-
Lygiakraštis trikampis
Trikampių rūšys pagal kampus
Pagal kampus trikampiai gali būti smailieji, statieji arba bukieji.
Statusis trikampis

Statusis trikampis – trikampis, kurio vienas kampas yra status.
Dešinėje pavaizduoto stačiojo trikampio ABC elementai:
- α, β – smailieji trikampio kampai;
- a, b -statiniai;
- c – įžambinė;
- aukštinė, nuleista iš stačiojo kampo viršūnės C į įžambinę;
- statinio a projekcija įžambinėje;
- statinio b projekcija įžambinėje;
- ;
Stačiojo trikampio statinis yra įžambinės ir to statinio projekcijos įžambinėje geometrinis vidurkis:
- ;
Stačiojo trikampio aukštinė, nubrėžta iš stačiojo kampo viršūnės, yra statinių projekcijų įžambinėje geometrinis vidurkis:
Prieš statųjį kampą esanti stačiojo trikampio kraštinė vadinama įžambine. Statųjį kampą sudarančios stačiojo trikampio kraštinės vadinamos statiniais. Stačiojo trikampio kraštinių ilgius sieja sąryšis, vadinamas Pitagoro teorema:
Stačiojo trikampio ploto formulės:
- ;
Jeigu trikampis yra status, tai jam galioja tokia taisyklė. Aukštinė, pakelta kvadratu, padalinusi trikampio pagrindą į dvi dalis yra lygi tų dviejų dalių sandaugai.
Smailusis ir bukasis trikampiai
Trikampis, kurio visi trys kampai smailieji, vadinamas smailiuoju trikampiu; trikampis, turintis vieną bukąjį kampą, vadinamas bukuoju trikampiu.
Trikampių savybės
Jeigu du trikampiai turi 2 vienodus kampus tuomet jie yra panašūs (skiriasi tik mastelis). Jeigu trikampiai turi du vienodus kampus ir vieną vienodo ilgio kraštinę, kuri yra ilgiausia, vidutinė arba trumpiausia pas abu trikampius, tada trikampiai yra tokie patys.
Jei trikampio vienas kampas yra C=90 laipsnių, o kitas kampas yra A=30 laipsnių, tai kraštinė a esanti priešais 30 laipsnių kampą yra dvigubai trumpesnė už įžambinę c, t. y. a=c/2. Pavyzdžiui, jei c=1, tai a=0,5. O kraštinė , esanti priešais kampą a.
Trikampio ploto apskaičiavimas

Geriausiai žinoma ir paprasčiausia trikampio ploto formulė yra
Čia S yra plotas, b – trikampio pagrindo ilgis, h – trikampio aukštinė.

Trikampio aukštinė h gali būti randama panaudojant trigonometriją. Vartojant tokį patį žymėjimą kaip dešinėje esančiame brėžinyje, trikampio aukštinės formulė yra h = a sin γ. Formulėje S = ½bh vietoje h įrašę a sin γ gauname kitą trikampio ploto formulę:
Čia α yra vidinis trikampio viršūnės A kampas, β – viršūnės B kampas ir γ – viršūnės C kampas.
Be to, sin α = sin (π – α) = sin (β + γ) ir t. t., todėl:
Herono formulė
Žinant visas tris trikampio kraštines a, b ir c, trikampio plotą galima paskaičiuoti pagal formulę:
Čia p yra trikampio pusperimetris. Jis lygus pusei trikampio perimetro:
Trikampio kraštinių ir kampų apskaičiavimas
Trigonometrinės funkcijos
Trigonometrinės funkcijos gali būti naudojamos stataus trikampio kraštinės ilgiui apskaičiuoti, kai yra žinomi trikampio kampai ir kuri nors viena kraštinė. Trigonometrines funkcijas galima apibrėžti taip (žymėjimai naudojami pagal dešinėje esantį trikampį):
Sinusas yra kraštinės esančios prieš kampą ir įžambinės santykis:

Kosinusas yra kraštinės esančios šalia kampo ir įžambinės santykis:
Tangentas yra statinio esančio priešais kampą santykis su statiniu esančiu prie kampo:
Taigi, jeigu, pavyzdžiui, žinome, kad kampas B = 60° ir kraštinė a = 5 cm, įžambinės c ilgį galime rasti pasinaudoję formule cos B = a/c, nes iš jos išplaukia, kad c = a/cos B = 5 cm/cos(60°) = 5 cm/0,5 = 10 cm.
Atvirkštinės trigonometrinės funkcijos
Atvirkštinės trigonometrinės funkcijos gali būti naudojamos vidiniams stačių trikampių kampams apskaičiuoti, kai yra žinomos bet kurios dvi trikampio kraštinės.

Arksinusas gali būti naudojamas apskaičiuoti kampui, kai yra žinomas stataus trikampio įžambinės ilgis ir kraštinės prieš ieškomą kampą ilgis. Kampas α yra lygus kraštinės prieš kampą α ir įžambinės santykio arksinusui:
Atitinkamai, kampas β lygus kraštinės prieš kampą β ir įžambinės santykio arksinusui:
Kampas α taip pat yra lygus kraštinės šalia kampo α ir įžambinės santykio arkkosinusui:
Arktangentas gali būti naudojamas apskaičiuoti kampams, kai yra žinomi abejų statinių ilgiai:
Kartais įžangoje į trigonometriją vietoje arcsin, arcos ir arctan rašoma atitinkamai sin−1, cos−1 ir tan−1. Aukštojoje matematikoje toks žymėjimas paprastai nenaudojamas, nes užrašą sin−1 (α) galima interpretuoti ir kaip 1/sin (α).
Kosinusų teorema

Kosinusų teorema dažniausiai naudojama rasti bet kokio trikampio kraštinėms ir (arba) kampus žinant dvi kraštines ir kampą tarp jų arba visas tris kraštines:
a, b ir c – kraštinių ilgiai, α – kampas tarp kraštinių b ir c, β – kampas tarp kraštinių a ir c, γ – kampas tarp kraštinių a ir b.
Jei trikampis statusis, tai vienanaris
virsta nuliu, nes 90 laipsnių kosinusas lygus nuliui. Tuomet kosinusų teorema tampa Pitagoro teorema. Dėl to ji kartais vadinama apibendrintąja Pitagoro teorema.
Jei yra žinomi visų trijų trikampio kraštinių ilgiai, kampai gali būti apskaičiuoti pagal formules:
Šios formulės yra nesunkiai išvedamos iš kosinusų teoremos.
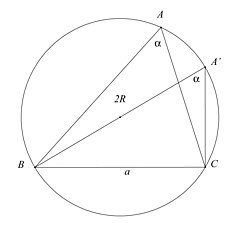
Sinusų teorema
Pagal sinusų teoremą galima rasti trikampio kraštines ir kampus žinant du kampus ir bent vieną kraštinę:
a, b ir c – kraštinių ilgiai,α, β ir γ – prieš jas esančių kampų dydžiai, o r- spindulys apibrėžtinio apskritimo.
Trikampiai neeuklidinėse geometrijose
Euklido plokštumoje trikampio vidinių kampų suma lygi 180°.
Neeuklidinėse geometrijose vidinių kampų suma nebūna lygi 180°. Pavyzdžiui, jeigu keliautojas, būdamas Šiaurės ašigalyje keliautų 10 000 km į pietus, tada 10 000 km į vakarus ir galiausiai 10 000 km atgal į šiaurę, jis grįžtų ten, iš kur išvyko, nors ir bus pasisukęs du kartus po 90°. Šio keliautojo nubrėžto trikampio kampų suma bus didesnė negu 80°, t. y. 270°. Taip yra dėl to, nes sferai (ji šiuo atveju yra gera geoido paviršiaus aproksimacija) galioja elipsinė geometrija, o ne Euklidinė. Ypatybė, kad Euklido erdvėje trikampio kampų suma yra 180°, yra pagrįsta penktąja Euklido aksioma (lygiagretumo postulatas), kuri išskiria Euklido geometriją iš kitų geometrijų.
Taip pat skaitykite
Šaltiniai
- ↑ Vaidotas Mockus. Geometrijos žinynas moksleiviams. – Šiauliai: Šiaulių pedagoginis institutas, 1996. – 34 p. ISBN 9986-38-010-3
- ↑ Autorių kolektyvas. Matematika 11. II dalis. – Vilnius: TEV, 2002. – 155 p. ISBN 9955-491-28-0
- ↑ Birutė Gražulevičienė. Mokyklinės matematikos žinynas. – Vilnius: Leidybos centras, 1997. – 75 p. ISBN 9986-03-264-4
- ↑ Autorių kolektyvas. Matematika 11. II dalis. – Vilnius: TEV, 2002. – 154 p. ISBN 9955-491-28-0
- ↑ Vaidotas Mockus. Geometrijos žinynas moksleiviams. – Šiauliai: Šiaulių pedagoginis institutas, 1996. – 31 p. ISBN 9986-38-010-3
- ↑ Autorių kolektyvas. Matematika 11. II dalis. – Vilnius: TEV, 2002. – 170 p. ISBN 9955-491-28-0












































