Oktaedras
| Taisyklingas oktaedras | |
|---|---|
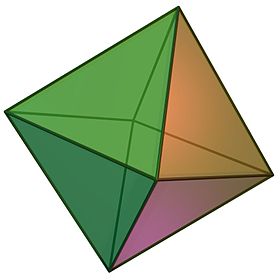 (Čia spustelėjus, suksis) | |
| Tipas | Platono kūnas |
| Elementai | F = 8, E = 12 V = 6 (χ = 2) |
| Sienos pagal puses | 8{3} |
| Konvėjaus užrašas | O aT |
| Šlėfli simbolis | {3,4} |
| r{3,3} or | |
| Vithofo simbolis | 4 | 2 3 |
| Kokseterio diagrama | |
| Simetrija | Oh, BC3, [4,3], (*432) |
| Sukinio grupė | O, [4,3]+, (432) |
| Indeksai | U05, C17, W2 |
| Savybės | taisyklingas iškilas deltaedras |
| Dvisienis kampas | 109.47122° = arccos(-1/3) |
 3.3.3.3 (Viršūnės planas) |
 Kubas (dualus briaunainis) |
 Išklotinė | |
Geometrijoje oktaedras – aštuoniasienis briaunainis. Taisyklingas oktaedras yra vienas iš Platono kūnų, kurį sudaro aštuoni lygiakraščiai trikampiai, po keturis susieinantys kiekvienoje viršūnėje, o prie kiekvienos viršūnės esančių plokščiųjų kampų suma lygi 240°.[1]
Taisyklingasis oktaedras yra dualus su kubu, arba kitaip sakant, oktaedras ir kubas (heksaedras) yra dualai. Jis yra rektifikuotas tetraedras. Šis briaunainis yra stačiakampė bipiramidė bet kuria stačiakampių koordinačių sistemos kryptimi. O taip pat ši figūra yra trikampė antiprizmė bet kuria iš keturių krypčių.
Oktaedras yra trimatė figūra, gaunama iš apibendrinto politopo, vadinamo hiperoktaedru (nenusistovėjęs terminas; angl. cross-polytope, orthoplex, hyperoctahedron, ar cocube)
Taisyklingas oktaedras yra trimatis rutulys, pagal Manhatano () metriką.
Šaltiniai
[redaguoti | redaguoti vikitekstą]- ↑ Vaidotas Mockus. Geometrijos žinynas moksleiviams. – Šiauliai: Šiaulių pedagoginis institutas, 1996. – 140 p. ISBN 9986-38-010-3


