Kvazitaisyklingasis briaunainis

Kvazitaisyklingosios geometrinės figūros

(3.3)2	(3.4)2	(3.5)2	(3.6)2	(3.7)2	(3.8)2	(3.∞)2
${\begin{Bmatrix}3\\3\end{Bmatrix}}$	${\begin{Bmatrix}3\\4\end{Bmatrix}}$	${\begin{Bmatrix}3\\5\end{Bmatrix}}$	${\begin{Bmatrix}3\\6\end{Bmatrix}}$	${\begin{Bmatrix}3\\7\end{Bmatrix}}$	${\begin{Bmatrix}3\\8\end{Bmatrix}}$	${\begin{Bmatrix}3\\\infty \end{Bmatrix}}$
r{3,3}	r{3,4}	r{3,5}	r{3,6}	r{3,7}	r{3,8}	r{3,∞}
Kvazitaisyklingasis briaunainis bei klojinys turi tik dvejopas taisyklingas sienas, kurios yra išsidėsčiusios aplink viršūnę pakaitomis. Jų viršūnės planas yra stačiakampis.

Geometrijoje, kvazitaisyklingasis briaunainis – toks pustaisyklingis briaunainis, kurio sienos griežtai yra tik dvejopi taisyklingieji daugiakampiai, kurie yra išsidėstę aplinkui viršūnę pakaitomis. Šių briaunainių briaunos yra tranzityvios, todėl jie yra taisyklingesni (artimesni taisyklingiems briaunainiams) negu pustaisyklingiai, kurių tik viršūnės yra tranzityvios.

Egzistuoja tik du iškili kvazitaisyklingieji briaunainiai: kuboktaedras ir ikosidodekaedras. Juos taip pavadino Johanas Kepleris, nustatęs, jog šios figūros turi abiejų susijusių dualų sienas – pirmu atveju, kubo ir oktaedro, antru, ikosaedro ir dodekaedro.

Šiems briaunainiams, kadangi juose yra išreikšta visa taisyklingų briaunainių duali pora, galima suteikti vertikalų Šlėfli simbolį ${\begin{Bmatrix}p\\q\end{Bmatrix}}$ arba r{p, q}, iš kurio matyti, kad figūra turi sienas atitinkančias taisyklingą briaunainį {p, q} ir taisyklingą jo dualą {q, p}. Tokiu simboliu žymimas kvazitaisyklingasis briaunainis turės viršūnės planą p.q.p.q (arba (p.q)²).

Apibendrintai, kvazitaisyklingosios figūros viršūnės planas yra (p.q)^r, kuriame r (=2 ar daugiau) rodo, kiek kartų abiejų sienų pora pasikartoja aplinkui viršūnę.

Klojiniai, išdėstyti plokštumoje, taip pat gali būti kvazitaisyklingieji, ypač dažniau sutinkami euklidinės erdvės triheksagoniniai klojiniai, kurių viršūnės planas yra (3.6)² – trikampio ir šešiakampio pora aplinkui viršūnę pasikartoja du kartus. Plačiai nagrinėjami ir atitinkami hiperbolinių plokštumų dariniai, pavyzdžiui, triheptagoniniai klojiniai (3.7)². Apibendrintai, klojinių viršūnės planas taip pat yra (p.q)², tik yra apribojimas 1/p+1/q<1/2 (kitaip jie nebebus klojiniai).

Kai kuriuos taisyklingus briaunainius ir klojinius (tuos, kurie turi lyginį sienų skaičių) galima laikyti kvazitaisyklingais, kadangi gretimas sienas teoriškai galima laikyti skirtingomis, pavyzdžiui, dažyti skirtinga spalva, nes jokios paviršiaus savybės nekeis jų vienodo išsidėstymo aplinkui viršūnę. Taigi, taisyklingą figūrą, kurios Šlėfli simbolis yra {p, q}, galima laikyti kvazitaisyklinga, kurios viršūnės planas yra (p.p)^q/2, jeigu tik q yra lyginis.

Oktaedrą galima laikyti kvazitaisyklinguoju tetratetraedru (du rinkiniai po keturis trikampius – po trikampę išorinę tetraedro sieną), (3_a.3_b)², ir trikampes sienas galima pakaitomis nudažyti dviem spalvomis. Panašiai, kvadratų klojinį (4_a.4_b)² galima laikyti kvazitaisyklinguoju ir nudažyti kaip šachmatų lentą. Lygiai taip pat trikampių klojinys (3_a.3_b)³ gali būti nudažytas dviem spalvomis.

Vithofo konstravimas

Taisyklingas (p | 2 q) ir kvazitaisyklingasis briaunainis (2 | p q) yra konstruojami pagal Vithofo konstrukcinę schemą, kai konstravimo taškas yra prie vieno iš 3 fundamentinės srities kampų.

Kokseteris (Coxeter) kvazitaisyklingąjį briaunainį apibrėžia kaip tą, kurio Vithofo simbolis yra p | q r, o jei q=2 arba q=r, šis briaunainis yra taisyklingas.

Kokseterio-Dinkino diagrama yra kitas simbolinis žymėjimo būdas, iš kurio galima matyti kvazitaisyklingą ryšį tarp dualios taisyklingų briaunainių poros:

Šlėfli simbolis		Kokseterio diagrama	Withofo simbolis
${\begin{Bmatrix}p,q\end{Bmatrix}}$	{p, q}		q | 2 p
${\begin{Bmatrix}q,p\end{Bmatrix}}$	{q, p}		p | 2 q
${\begin{Bmatrix}p\\q\end{Bmatrix}}$	r{p, q}		2 | p q

Iškili kvazitaisyklingieji briaunainiai ir klojiniai

Egzistuoja tik du iškili kvazitaisyklingieji briaunainiai:

1. Kuboktaedras ${\begin{Bmatrix}3\\4\end{Bmatrix}}$, kurio viršūnės planas yra (3.4)², o Kokseterio-Dinkino diagrama
2. Ikosidodekaedras ${\begin{Bmatrix}3\\5\end{Bmatrix}}$, kurio viršūnės planas yra (3.5)², o Kokseterio-Dinkino diagrama

Dera pridurti, kad oktaedras, kuris įprastai laikomas taisyklingu, ${\begin{Bmatrix}3\\3\end{Bmatrix}}$, kurio viršūnės planas yra (3.3)², lygia greta gali būti laikomas ir kvazitaisyklingu, jeigu kas antrą sieną nudažysime dviem skirtingomis spalvomis. Toks oktaedras paprastai vadinamas tetratetraedru. Visų kitų taisyklingųjų briaunainių viršūnės plane yra nelyginis skaičius daugiakampių, tad jų neįmanoma taip nudažyti, kad jų briaunos taptų tranzityvios. Kvazitaisyklingųjų briaunainių Kokseterio-Dinkino diagrama yra .

Kiekvienas jų atspindi taisyklingų briaunainių dualią porą. Abiejų kvazitaisyklingų briaunainių pavadinimuose yra užuomina į susijusią dualią porą: kuboktaedras = kubas + oktaedras, o ikosidodekaedras = ikosaedras + dodekaedras. Oktaedras atitinka tetratetraedrą, kuris atspindi du pačius sau dualius tetraedrus, sudarančius figūrą, vadinamą stella octangula.

Taisyklingas	Dualus taisyklingas	Kvazitaisyklingasis	Viršūnės planas
Tetraedras {3,3} 3 | 2 3	Tetraedras {3,3} 3 | 2 3	Tetratetraedras r{3,3} 2 | 3 3	3.3.3.3
Kubas {4,3} 3 | 2 4	Oktaedras {3,4} 4 | 2 3	Kuboktaedras r{3,4} 2 | 3 4	3.4.3.4
Dodekaedras {5,3} 3 | 2 5	Ikosaedras {3,5} 5 | 2 3	Ikosidodekaedras r{3,4} 2 | 3 5	3.5.3.5

Kiekvienas iš šių kvazitaisyklingųjų briaunainių gali būti sukonstruotas rektifikuojant kurį nors taisyklingą pirminį briaunainį, tai yra visiškai nupjaunant briaunas, kol pirminės briaunos virsta tašku (rektifikuojamos į tašką).

Kvazitaisyklingieji klojiniai

Kvazitaisyklingiesiems briaunainiams galima priskirti ir klojinius iš dviejų skirtingų taisyklingų daugiakampių. Tokie yra triheksagonaliniai klojiniai, kurių viršūnės planas yra 3.6.3.6 – tai kvazitaisyklingieji klojiniai sudaryti iš taisyklingų trikampių ir šešiakampių sujungtų į plokščią klojinį.

Taisyklingas	Dualus taisyklingas	Kvazitaisyklingasis	Viršūnės planas
Šešiakampis klojinys {6,3} 6 | 2 3	Trikampis klojinys {3,6} 3 | 2 6	Triheksagoninis klojinys r{5,3} 2 | 3 6	3.6.3.6

Šachmatų lentos raštas yra kvazitaisyklingas spalvinimas, pritaikytas taisyklingam kvadratų klojiniui, kurio viršūnės planas yra 4.4.4.4:

Taisyklingas	Dualus taisyklingas	Kvazitaisyklingasis	Viršūnės planas
{4,4} 4 | 2 4	{4,4} 4 | 2 4	r{4,4} 2 | 4 4	4.4.4.4

Trikampį klojinį taip pat galima laikyti kvazitaisyklingu, kuriame aplinkui kiekvieną viršūnę išsidėsto trys dvispalvių trikampių rinkiniai – (3.3)³:

h{6,3} 3 | 3 3 =

Hiperbolinėje plokštumoje šių figūrų seka plečiasi, pavyzdžiui, prisideda triheptagoniniai klojiniai (viršūnės planas 3.7.3.7) ir pan.

Taisyklingas	Dualus taisyklingas	Kvazitaisyklingasis	Viršūnės planas
Heptagonal tiling {7,3} 7 | 2 3	Triangular tiling {3,7} 3 | 2 7	Triheptagonal tiling r{3,7} 2 | 3 7	3.7.3.7

Neiškili pavyzdžiai

Kokseteris kai kuriuos žvaigždinius briaunainius priskiria prie kvazitaisyklingųjų:

Du yra vediniai iš dualių Keplerio-Puanso kūnų porų, panašiai, kaip iškilųjų – tai didysis ikosidodekaedras ${\begin{Bmatrix}3\\5/2\end{Bmatrix}}$ ir dodekadodekaedras ${\begin{Bmatrix}5\\5/2\end{Bmatrix}}$:

Taisyklingas	Dualus taisyklingas	Kvazitaisyklingasis	Viršūnės planas
Didysis žvaigždinis dodekaedras {5/2,3} 3 | 2 5/2	Didysis ikosaedras {3,5/2} 5/2 | 2 3	Didysis ikosidodekaedras r{3,5/2} 2 | 3 5/2	3.5/2.3.5/2
Mažasis žvaigždinis dodekaedras {5/2,5} 5 | 2 5/2	Didysis dodekaedras {5,5/2} 5/2 | 2 5	Dodekadodekaedras r{5,5/2} 2 | 5 5/2	5.5/2.5.5/2

Trečias yra ditrigoninės formos briaunainis, kurio viršūnės planą sudaro triskart pasikartojanti dviejų sienų pora:

Vaizdas	Briaunainio pavadinimas Withofo simbolis Kokseterio diagrama	Viršūnės planas
	Ditrigoninis dodekadodekaedras 3 | 5/3 5 or	(5.5/3)3
	Mažasis ditrigoninis ikosidodekaedras 3 | 5/2 3 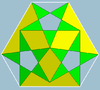or	(3.5/2)3
	Didysis ditrigoninis ikosidodekaedras 3/2 | 3 5 or	((3.5)3)/2

Kvazitaisyklingieji dualai

Kai kurie autoriai teigia, kad kvazitaisyklingųjų briaunainių dualai, kadangi turi tą pačią simetriją, kaip pirminiai kūnai, irgi turi būti kvazitaisyklingi. Bet ne visi su tuo sutinka. Šie dualai turi tranzityvias briaunas ir sienas (bet netranzityvias viršūnes); tad jie yra Katalano kūnai su tranzityviomis briaunomis. Iškilieji kvazitaisyklingųjų briaunainių dualai, atitinkamai aukščiau pateiktai tvarkai, yra:

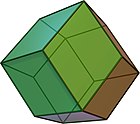
1. Rombinis dodekaedras, turintis dviejų tipų pakaičiui einančias viršūnes, iš kurių 8 turi tris rombines sienas ir 6 – keturias rombines sienas.
2. Rombinis triakontaedras, turintis dviejų tipų pakaičiui einančias viršūnes, iš kurių 20 turi tris rombines sienas ir 12 – penkias rombines sienas.

Papildomai, atsižvelgiant į „dvispalvio“ oktaedro dualumą, kvazitaisyklinguoju galima laikyti kubą, kuris įprastai yra taisyklingasis briaunainis, jei jo viršūnes pakaičiui nuspalvinsime dviem skirtingomis spalvomis.

Jų sienų konfigūracija turės pavidalą V3.n.3.n, o Kokseterio-Dinkino diagrama bus .

Kubas V(3.3)2	Rombinis dodekaedras V(3.4)2	Rombinis triakontaedras V(3.5)2	Rombinis klojinys V(3.6)2	V(3.7)2	V(3.8)2

Visi trys kvazitaisyklingieji dualai turi jiems būdingas rombines sienas.

Tas pats rombinių sienų išsidėstymas kartojasi klojinyje kaip V(3.6)².

Šaltiniai

• Cromwell, P. Polyhedra, Cambridge University Press (1977).
• Coxeter, Regular Polytopes, (3rd edition, 1973), Dover edition, ISBN 0-486-61480-8, 2.3 Quasi-Regular Polyhedra. (p. 17), Quasi-regular honeycombs p.69