Katalano kūnas

Rombinis dodekaedras ir jo sienos konfigūracija.

„Disdyakis“ triakontaedras, kurio sienos konfigūracija V4.6.10, yra didžiausias Katalano kūnas, turintis 120 sienų.

Matematikoje Katalano kūnas – atitinkamo Archimedo kūno dualusis briaunainis. Katalano kūnai taip vadinami pagal juos 1865 m. pirmą kartą aprašiusį belgų matematiką Euženą Katalaną (Eugène Catalan).

Katalano kūnai yra iškilieji briaunainiai. Jie yra tranzityvūs sienų atžvilgiu, bet netranzityvūs briaunų atžvilgiu. Taip yra todėl, kad šių kūnų dualai, Archimedo kūnai, yra tranzityvūs briaunų atžvilgiu, bet netranzityvūs sienų atžvilgiu. Reikia pastebėti, kad skirtingai negu Platono kūnai ir Archimedo kūnai, Katalano kūnų sienos nėra taisyklingieji daugiakampiai. Kita vertus, Katalano kūnų viršūnių planai yra taisyklingieji daugiakampiai ir jie turi pastovius dvisienius kampus. Kadangi jų sienos yra tranzityvios, Katalano kūnai yra izoedrai.

Be to, du Katalano kūnai yra dar tranzityvūs ir briaunų atžvilgiu: rombinis dodekaedras ir rombinis triakontaedras. Šiuodvi figūros yra dviejų kvazitaisykligų Archimedo kūnų dualai.

Lygiai, kaip prizmės ir antiprizmės bendruoju atveju nėra priskiriamos prie Archimedo kūnų, taip bipiramidės ir trapecoedrai nepriskiriami prie Katalano kūnų, nors abiejų klasių figūros yra tranzityvios sienų atžvilgiu.

Dviem Katalano kūnams būdingas chirališkumas: penkiakampiam ikositetraedrui ir penkiakampiam heksakontaedrui, kurie yra atitinkamai dualūs su nusklembtu kubu ir nusklembtu dodekaedru. Kiekvienas šių dualų iš tiesų yra enantiomorfų pora. Bet neskaičiuojant šių enantiomorfų ir bipiramidžių bei trapecoedrų iš viso turime 13 Katalano kūnų.

nr.	Archimedo kūnai	Katalano kūnai
1	Nupjautinis tetraedras	„Triakis“ tetraedras
2	Nupjautinis kubas	„Triakis“ oktaedras
3	Nupjautinis kuboktaedras	„Disdyakis“ dodekaedras
4	Nupjautinis oktaedras	„Tetrakis“ heksaedras
5	Nupjautinis dodekaedras	„Triakis“ ikosaedras
6	Nupjautinis ikosidodekaedras	„Disdyakis“ triakontaedras
7	Nupjautinis ikosaedras	„Pentakis“ dodekaedras
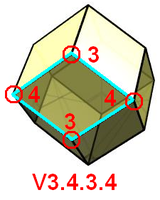
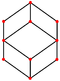
8	Kuboktaedras	Rombinis ddodekaedras
9	Ikosidodekaedras	Rombinis triakontaedras
10	Rombinis kuboktaedras	Deltoidinis ikositetraedras
11	Rombinis ikosidodekaedras	Deltoidinis heksakontaedras
12	Nusklembtas kubas	Penkiakampis ikositetraedras
13	Nusklembtas dodekaedras	Penkiakampis heksakontaedras

„Triakis“ (ir kitos panašios Katalano kūnų pavadinimo dalys) yra hibridinis darinys iš graikų τρι, tri – „trys“ ir lotynų acis „ketera“, „smailė“; taigi „triakis“ tetraedras yra tetraedras, kurio kiekvienoje sienoje iškilusios trys briaunos („keteros“). Atitinkamai „tetrakis“ reiškia sieną, kurioje iškilusios keturios (tetra), „pentakis“ – penkios briaunos, sudarančios lygiašonius trikampius, o „disdyakis“ – briaunos sudaro įvairiakraščius trikampius.

Simetrija

Katalano kūnus, kaip ir jiems dualius Archimedo kūnus galima sugrupuoti pagal simetrijos klases: tetraedrines, oktaedrines, ikosaedrines simetrijos kūnus. Kiekvienoje simetrijos klasėje yra po šešis kūnus, o kadangi tetraedrinės simetrijos grupės kūnams būdinga simetrija pačiam sau, čia yra tik trys kūnai, du iš kurių dubliuoja oktaedrinės simetrijos kūnai. Taigi 6+6+3-2=13.

Tetraedrinė simetrija Archimedo kūnai Katalano kūnai

Oktaedrinė simetrija Archimedo kūnai Katalano kūnai

Ikosaedrinė simetrija

Archimedo kūnai
Katalano kūnai

Sąrašas

Pavadinimas (Dvigubas) Konvėjaus žymėjimas	Vaizdas	Ortogonalinis karkasas	Sienos daugiakampis	Sienos	Briaunos	Viršūnės	Simetrija
„Triakis“ tetraedras (nupjautinis tetraedras) „kT“			Lygiašonis V3.6.6	12	18	8	Td
Rombinis dodekaedras (kuboktaedras) „jC“			Rombas V3.4.3.4	12	24	14	Oh
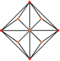
„Triakis“ oktaedras (nupjautinis kubas) „kO“			Lygiašonis V3.8.8	24	36	14	Oh
„Tetrakis“ heksaedras (nupjautinis oktaedras) „kC“			Lygiašonis V4.6.6	24	36	14	Oh
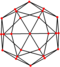
Deltoidinis ikositetraedras (rombinis kuboktaedras) „oC“			Aitvaras V3.4.4.4	24	48	26	Oh
„Disdyakis“ dodekaedras (nupjautinis kuboktaedras) „mC“			Įvairiakraštis V4.6.8	48	72	26	Oh
Penkiakampis ikositetraedras (nusklembtas kubas) „gC“			Penkiakampis V3.3.3.3.4	24	60	38	O
Rombinis triakontaedras (ikosidodekaedras) „jD“			Rombas V3.5.3.5	30	60	32	Ih
„Triakis“ ikosaedras (nupjautinis dodekaedras) „kI“			Lygiašonis V3.10.10	60	90	32	Ih
„Pentakis“ dodekaedras (nupjautinis ikosaedras) „kD“			Lygiašonis V5.6.6	60	90	32	Ih
Deltoidinis heksakontaedras (rombinis ikosidodekaedras) „oD“			Aitvaras V3.4.5.4	60	120	62	Ih
„Disdyakis“ triakontaedras (nupjautinis ikosidodekaedras) „mD“			Įvairiakraštis V4.6.10	120	180	62	Ih
Penkiakampis heksakontaedras (nusklembtas dodekaedras) „gD“			Penkiakampis V3.3.3.3.5	60	150	92	I

Šaltiniai

• Eugène Catalan Mémoire sur la Théorie des Polyèdres. J. l'École Polytechnique (Paris) 41, 1-71, 1865.
• Alan Holden Shapes, Space, and Symmetry. New York: Dover, 1991.
• Wenninger, Magnus (1983), Dual Models, Cambridge University Press, ISBN 978-0-521-54325-5  (The thirteen semiregular convex polyhedra and their duals)
• Williams, Robert (1979). The Geometrical Foundation of Natural Structure: A Source Book of Design. Dover Publications, Inc. ISBN 0-486-23729-X.  (Section 3-9)
• Anthony Pugh (1976). Polyhedra: A visual approach. California: University of California Press Berkeley. ISBN 0-520-03056-7. Chapter 4: Duals of the Archimedean polyhedra, prisma and antiprisms

Nuorodos

• Weisstein, Eric W., „Catalan Solids“, MathWorld.
• Weisstein, Eric W., „Isohedron“, MathWorld.
• Olshevsky, George, Catalan at Glossary for Hyperspace.
• Archimedean duals – at Virtual Reality Polyhedra
• Interactive Catalan Solid Archyvuota kopija 2005-12-01 iš Wayback Machine projekto. in Java