Keplerio-Puanso kūnas
 Kiekvienam briaunainiui nurodytas Šlėfli simbolis, kurio pavidalas {p, q}, ir konkretus pavadinimas. Viena briaunainio sienų nuspalvinta geltonai, kad aiškiau matytųsi, kaip jos išsidėsčiusios. |
Keplerio–Puanso kūnas (Kepler–Poinsot kūnas) – kiekvienas iš keturių geometrinių kūnų, kurie yra taisyklingieji žvaigždiniai briaunainiai[1]
Šie kūnai konstruojami iš taisyklingo dodekaedro arba ikosaedro, vykstant stelacijai, o nuo pirminių iškilių briaunainių jie skiriasi tuo, kad Keplerio-Puanso kūnai turi būdingą viršūnės planą – pentagramą.
Stelacija – tai veiksmas, kai iš briaunainio sienos iškyla tos sienos daugiakampį atitinkanti žvaigždė. Visiems žvaigždiniams briaunainiams būdinga, kad sienos sudaro įvairiakampes žvaigždes, bet tik šie keturi žvaigždiniai Keplerio-Puanso kūnai turi visas taisyklingųjų briaunainių savybes.
Savybės[redaguoti | redaguoti vikitekstą]
Neiškilumas[redaguoti | redaguoti vikitekstą]
Šių briaunainių sienos arba viršūnės planai yra pentagramos (žvaigždiniai penkiakampiai). Mažasis žvaigždinis dodekaedras ir didysis žvaigždinis dodekaedras – tai briaunainiai, kurių sienos yra neiškili žvaigždiniai penkiakampiai, o didysis dodekaedras ir didysis ikosaedras – tai briaunainiai, kurių sienos yra iškili penkiakampiai, bet jų viršūnės planas yra žvaigždiniai penkiakampiai.
Visų keturių briaunainių dvi sienos kertasi išilgai linijos, kuri nėra kurios nors sienos kraštinė, taigi dalis kiekvienos sienos eina briaunainio vidumi. Ši kirtimosi linija nėra briaunainio paviršiaus dalis ir kartais vadinama netikrąja briauna. Lygia taip pat, kai šios linijos susikerta kitur nei sienos kampas, susikirtimo taškas vadinamas netikrąja višrūne. Žemiau pateiktuose raudonuose briaunainių modeliuose tikrosios viršūnės pažymėtos auksiniais bumbulais, o sidabriniai strypeliai žymi tikrąsias briaunas. Mažojo ir didžiojo žvaigždinio dodekaedro modeliuose aiškiai matome netikrąsias viršūnes, didžiojo dodekaedro – netikrąsias briaunas, o didžiojo ikosaedro – tiek netikrąsias viršūnes, tiek netikrąsias briaunas.
Smulkiau nagrinėdami šiuos modelius matome, kad mažasis žvaigždinis dodekaedras turi 12 penkiakampės žvaigždės sienų, kurių centrinės dalies iškilas penkiakampis slepiasi figūros viduje. Regimąją kiekvienos sienos dalį sudaro 5 lygiakraščiai trikampiai, liečiantys vienas kitą penkiuose taškuose aplinkui vidinį (paslėptą) penkiakampį. Šių trikampių visumą galima laikyti 60-čia briaunainio sienų, taip sutapatindami figūrą su nauju, netaisyklingu briaunainiu, kuris išoriškai yra tapatus nagrinėjamajam. Tuomet kiekviena mažojo žvaigždinio dodekaedro briauna bus padalinta į tris trumpesnes (dvejopas) briaunas, o 20 netikrųjų viršūnių taps tikrosiomis ir iš viso turėsime 32 viršūnes (ir vėl dvejopas). Šiuo atveju vidiniai neregimieji penkiakampiai daugiau nebebus laikomi briaunainio paviršiaus dalimis ir bus galima juos ignoruoti. Nuo šiol Oilerio charakteristika bus: 60 − 90 + 32 = 2. Bet šio briaunainio jau nebegalima laikyti briaunainiu, kurį nusako Šlėfli simbolis {5/2, 5}, tad kartu, jo nebegalima laikyti Keplerio-Puanso kūnu, nors išoriškai jis niekaip nepakito. Tiesiog pasikeitė matematinės jo egzistavimo sąlygos.
Oilerio charakteristika χ[redaguoti | redaguoti vikitekstą]
Keplerio-Puanso kūnus apibrėžtinė sfera gaubia dvejopai, vienaip, kai gaubimo taškais yra penkiakampių sienų centriniai taškai, ir kitaip, kai gaubimo taškai yra viršūnės. Todėl jie nebūtinai yra tokie topologiškai ekvivalentiški sferai, kaip Platono kūnai. Ir, iš dalies, Oilerio formulė briaunainiams
ne visuomet yra teisinga. Šlėfli laikėsi nuomonės, kad briaunainis privalo atitikti lygybę χ = 2 ir jis atmetė mažąjį žvaigždinį dodekaedrą ir didįjį dodekaedrą, kaip netikrus briaunainius. Bet šis požiūris nebuvo plačiai pripažintas.
Kai Arturas Kailėjus (Arthur Cayley) rado būdą modifikuoti Oilerio formulę, įtraukiant į ją politopo tankį D, ir atsižvelgti į viršūnės plano tankį () ir sienų tankį (), tada paaiškėjo, kad vis dėlto tiek iškilių briaunainių, tiek Keplerio-Puanso kūnų
Dualumas[redaguoti | redaguoti vikitekstą]
Keplerio-Puanso kūnai susiję tarpusavyje dualumo savybe ir sudaro dualų poras:
- mažasis žvaigždinis dodekaedras ir didysis dodekaedras;
- didysis žvaigždinis dodekaedras ir didysis ikosaedras.
Bendri duomenys apie Keplerio-Puanso kūnus[redaguoti | redaguoti vikitekstą]
| Pavadinimas | Vaizdas | Sferinis klojinys |
Stelacijos diagrama |
Šlėfli simbolis {p, q} ir Kokseterio diagrama |
Sienos {p} |
Briaunos | Viršūnės {q} |
Viršūnės plano konfigūracija |
χ | Politopo tankis D | Simetrijos grupė | Dualas |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Mažasis žvaigždinis dodekaedras | 
|

|

|
{5/2,5} |
12 {5/2} |
30 | 12 {5} |
 (5/2)5 |
-6 | 3 | Ih | Didysis dodekaedras |
| Didysis žvaigždinis dodekaedras | 
|

|

|
{5/2,3} |
12 {5/2} |
30 | 20 {3} |
 (5/2)3 |
2 | 7 | Ih | Didysis ikosaedras |
| Didysis dodekaedras | 
|

|

|
{5,5/2} |
12 {5} |
30 | 12 {5/2} |
 (55)/2 |
-6 | 3 | Ih | Mažasis žvaigždinis dodekaedras |
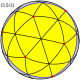
| Didysis ikosaedras | 
|
|

|
{3,5/2} |
20 {3} |
30 | 12 {5/2} |
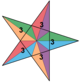 (35)/2 |
2 | 7 | Ih | Didysis žvaigždinis dodekaedras |
Sąsaja tarp taisyklingųjų briaunainių[redaguoti | redaguoti vikitekstą]
| Briaunainiai su vienodai išsidėsčiusiomis viršūnėmis: | Briaunainiai su vienodai išsidėsčiusiomis viršūnėmis ir briaunomis: |
|---|---|
    ikosaedras, mažasis žvaigždinis dodekaedras, didysis ikosaedras ir didysis dodekaedras. |
  mažasis žvaigždinis dodekaedras ir didysis ikosaedras. |
  dodekaedras ir didysis žvaigždinis dodekaedras. |
  ikosaedras ir didysis dodekaedras. |
Vienodai išsidėsčiusias viršūnes ir briaunas poromis turi:
- Mažasis žvaigždinis dodekaedras ir didysis ikosaedras
- Ikosaedras ir didysis dodekaedras
Stelacija: trys neiškili dodekaedrai yra taisyklingo iškilo dodekaedro stelacija:
- mažasis žvaigždinis dodekaedras;
- didysis žvaigždinis dodekaedras;
- didysis dodekaedras;
o neiškilas ikosaedras yra taisyklingo iškilo ikosaedro stelacija:
- didysis ikosaedras.
Išduobimas: du neiškili Keplerio-Puanso kūnai yra taisyklingo iškilo dodekaedro išduobimas:
- mažasis žvaigždinis dodekaedras;
- didysis ikosaedras;
o kiti du Keplerio-Puanso kūnai (didieji dodekaedrai) yra taisyklingo iškilo ikosaedro išduobimas:
- didysis žvaigždinis dodekaedras;
- didysis dodekaedras.
Kai laikoma, kad sienos susikirsdamos sukuria naujas briaunas ir viršūnes, taip gautos figūros matematiškai nebelaikomos taisyklingomis, bet jos vis dar laikomos žvaigždiniais briaunainiais, kuriems galioja stelacijos taisyklės. Šią problemą nagrinėja Magnusas Veningeris[2]
Istorija[redaguoti | redaguoti vikitekstą]

Nemaža Keplerio-Puanso kūnų (gal net visi) buvo žinoma dar iki Keplerio. Mažasis žvaigždinis dodekaedras pavaizduotas Venecijos šv. Marko bazilikos marmurinėje grindų mozaikoje. Laikoma, kad ši mozaika sukurta XV a., nes XVI a. ksilografinėje knygoje, Perspectiva corporum regularium ('Taisyklingųjų kūnų perspektyvos'), kurios autorius Paolas Učelas (Paolo Uccello), yra didžiojo dodekaedro ir didžiojo žvaigždinio dodekaedro graviūros[3]. Kita vertus iš knygos aiškėja, kad taisyklingaisiais laikyti tik penki Platono kūnai, o čia pavaizduotų didžiųjų dodekaedrų taisyklingumas nepripažįstamas.
Kartais tik mažasis ir didysis žvaigždiniai dodekaedrai vadinami Keplerio briaunainiais, nes pirmasis 1619 metais jų taisyklingumą aprašė Johanas Kepleris. Jis juos gavo stelacijos būdu iš taisyklingo iškilo dodekaedro ir pirmą kartą nagrinėjo juos kaip paviršių, o ne vientisą tūrinį kūną. Mokslinikas atkreipė dėmesį, kad iškeliant iškilo dodekaedro briaunas arba sienas, kol jos vėl susikerta, galima gauti žvaigždinius penkiakampius. Po to jis nustatė, kad šios penkiakampės žvaigždės taip pat yra taisyklingos. Šitaip jis sukonstravo du žvaigždinius briaunainius. Kiekvieno jų siena per vidurį buvo neįdubusi, nors ir pasislėpusi briaunainio viduje, o matėsi tik kyšančios trikampės žvaigždžių smailės. Galiausiai Kepleris priėjo išvadą, kad šie briaunainiai tenkina taisyklingumo reikalavimus, nepaisant, kad jie nebuvo iškili, kaip tradiciniai Platono kūnai.
1809 metais Lui Puanso (Louis Poinsot) iš naujo atrado Keplerio aprašytas figūras, konstruodams penkiakampes žvaigždes aplinkui kiekvieną viršūnę. Jis taip pat sukonstravo iškilus daugiakampius apie žvaigždės viršūnes ir aptiko dar dvi taisyklingas žvaigždes: didijį ikosaedrą ir didijį dodekaedrą. Kai kada šios dvi figūros vadinamos Puanso briaunainiais. Bet Puanso nebuvo tikras, ar daugiau nėra taisyklingų žvaigždinių briaunainių.
Po trejų metų Ogustinas Koši (Augustin Cauchy) įrodė, kad daugiau neįmanoma iš Platono kūnų sukurti taisyklingų žvaigždžių. Beveik po pusės šimtmečio, 1858 metais, Žoze Bertranas (Joseph Louis François Bertrand), naudodamasis sienų išduobimu, pateikė dar elegantiškesnį įrodymą, kad daugiau tokių taisyklingų kūnų neegzistuoja.
Tuoj po metų Arturas Kajlis (Arthur Cayley) suteikė Keplerio-Puanso kūnams pavadinimus, kurie prigijo ir naudojami iki šiol. Praėjus šimtmečiui, XX a. pradžioje, Džonas Konvėjus (John Horton Conway) sukūrė sisteminę stelacijos terminologiją, kuri apėmė sąvokas iki matematinių ketvirto matavimo reiškinių. Savo schemoje jis pasiūlė truputėlį kitokius Keplerio-Puanso kūnų pavadinimus:
| Kajlio pavadinimai | Konvėjaus pavadinimai |
| mažasis žvaigždinis dodekaedras | žvaigždinis dodekaedras |
| didysis dodekaedras | didysis dodekaedras (toks pat) |
| didysis žvaigždinis dodekaedras | žvaigždinis didysis dodekaedras |
| didysis ikosaedras | didysis ikosaedras (toks pat) |
Nors Konvėjaus pavadinimai kartais vartojami, jie plačiai nepaplito.
Taisyklingi žvaigždiniai briaunainiai mene ir kultūroje[redaguoti | redaguoti vikitekstą]

Taisyklingus žvaigždinius briaunainius pirmiausia aptinkame renesanso mene. Mažasis žvaigždinis dodekaedras vaizduojamas Venecijos baziliką puošiančioje marmurinėje grindų mozaikoje (apie 1430 m.). 1568 metais išleista ksilografinė knyga, kurioje yra didžiojo dodekaedro ir didžiojo žvaigždinio dodekaedro graviūros. Tiesa, antrasis briaunainis truputį iškraipytas, greičiausiai dėl naudoto vaizdavimo būdo, o ne dėl to, kad menininkas prastai suprato jo formą. Bet nėra jokių įrodymų, kad menininkai suprato, kad šios figūros yra tokios pat taisyklingos, kaip Platono kūnai.
Žinomas XX a. įmantrių geometrinių formų piešėjas, Morisas Kornelijus Ešeris, dažnai vaizduodavo taisyklinguosius geometrinius kūnus. Jo litografijoje „Gravitacija“ (1952 m.), vaizduojamas mažasis žvaigždinis dodekaedras.
Didžiojo dodekaedro fragmentų dėlionė panaudota XX a. 9 dešimtmetyje sukurtame galvosūkyje „Aleksandro žvaigždė“, panašiame į Rubiko kubą.
Prie Norvegijos sostinės Oslo Gardermoeno oro uosto pastatyta menininko Vebjorno Sando (Vebjørn Sand) skulptūra, pavadinta „Keplerio žvaigždė“ (kitaip dar vadinama „Norvegijos taikos žvaigžde“ ar tiesiog „Taikos žvaigžde“). Skulptūros aukštis yra 14 metrų, o ją sudaro trys grakščios keturbriaunės kolonos, ant kurių iškelta didžiulė žvaigždė – vienas į kitą įmontuoti ikosaedras ir dodekaedras, įdėti į didįjį žvaigždinį dodekaedrą.
Nuorodos[redaguoti | redaguoti vikitekstą]
- ↑ Coxeter, Star polytopes and the Schläfli function f{α,β,γ}, p. 121
- ↑ Wenninger, Magnus (1974). Polyhedron Models. Cambridge University Press. ISBN 0-521-09859-9.
- ↑ Perspectiva corporum regularium Archyvuota kopija 2016-10-13 iš Wayback Machine projekto.
- J. Bertrand, Note sur la théorie des polyèdres réguliers, Comptes rendus des séances de l’Académie des Sciences, 46 (1858), pp. 79–82, 117.
- Augustin Louis Cauchy, Recherches sur les polyèdres. J. de l'École Polytechnique 9, 68-86, 1813.
- Arthur Cayley, On Poinsot’s Four New Regular Solids. Philos. Mag. 17, pp. 123–127 and 209, 1859.
- John H. Conway, Heidi Burgiel, Chaim Goodman-Strauss, The Symmetry of Things 2008, ISBN 978-1-56881-220-5 (Chapter 24, Regular Star-polytopes, pp. 404–408)
- Kaleidoscopes: Selected Writings of H. S. M. Coxeter, edited by F. Arthur Sherk, Peter McMullen, Anthony C. Thompson, Asia Ivic Weiss, Wiley-Interscience Publication, 1995, ISBN 978-0-471-01003-6 [1]
- (Paper 1) H.S.M. Coxeter, The Nine Regular Solids [Proc. Can. Math. Congress 1 (1947), 252–264, MR 8, 482]
- (Paper 10) H.S.M. Coxeter, Star Polytopes and the Schlafli Function f(α,β,γ) [Elemente der Mathematik 44 (2) (1989) 25–36]
- P. Cromwell, Polyhedra, Cabridgre University Press, Hbk. 1997, Ppk. 1999.
- Theoni Pappas, (The Kepler–Poinsot Solids) The Joy of Mathematics. San Carlos, CA: Wide World Publ./Tetra, p. 113, 1989.
- Louis Poinsot, Memoire sur les polygones et polyèdres. J. de l'École Polytechnique 9, pp. 16–48, 1810.
- Lakatos, Imre; Proofs and Refutations, Cambridge University Press (1976) – discussion of proof of Euler characteristic
- Wenninger, Magnus (1983). Dual Models. Cambridge University Press. ISBN 0-521-54325-8., pp. 39–41.
- John H. Conway, Heidi Burgiel, Chaim Goodman-Strass, The Symmetries of Things 2008, ISBN 978-1-56881-220-5 (Chapter 26. pp. 404: Regular star-polytopes Dimension 3)
- Anthony Pugh (1976). Polyhedra: A Visual Approach. California: University of California Press Berkeley. ISBN 0-520-03056-7. Chapter 8: Kepler Poisot polyhedra




