Pitagoro teorema

Vaizdinis paaiškinimas su vandens indais. Visas vanduo iš dviejų viršutinių indų be liekanos ir pertekliaus suteka į apatinį.

Pitagoro teorema – teorema, kuri teigia, jog stataus trikampio statinių kvadratų suma yra lygi įžambinės kvadratui:

$a^{2}+b^{2}=c^{2}$

kur a ir b yra trikampio statinių ilgiai, o c – įžambinės ilgis. Ši lygtis vadinama Pitagoro lygtimi, o ją tenkinantys sveikieji skaičiai (pavyzdžui, 3, 4, 5) – Pitagoro trejetais.

Pavyzdžiui, jei a = 8, o b = 6, tai $c={\sqrt {a^{2}+b^{2}}}={\sqrt {8^{2}+6^{2}}}={\sqrt {64+36}}={\sqrt {100}}=10$

Atvirkštinė Pitagoro teorema: jeigu trikampio vienos kraštinės kvadratas yra lygus kitų dviejų kraštinių kvadratų sumai, tai tas trikampis yra statusis.

Pitagoro teorema taip pat yra atskiras kosinusų teoremos atvejis, kai kampas yra statusis.

Istorija

Iki šiol nesutariama, ar graikų filosofo ir matematiko Pitagoro vardu teorema buvo atrasta vieną kartą, ar daug kartų daugelyje pasaulio vietų, taip pat nėra aiški pirmojo atradimo ir įrodymo data. Mesopotamijos matematikos istorikai priėjo išvados, jog Pitagoro teorema buvo plačiai žinoma Senojo Babilono karalystėje (XX–XVI a. pr. m. e.), tai yra daugiau kaip tūkstantis metų iki Pitagoro gimimo. Teoremos istoriją galima suskirstyti į keturias dalis: Pitagoro trejetų, stačiojo trikampio kraštinių santykių, gretimų kampų ryšių žinios ir teoremos įrodymai tam tikroje dedukcinėje sistemoje.

Mesopotamija

Plimpton 322 lentelė.

Yra įrodymų, kad senovės babiloniečiai jau žinojo Pitagoro teoremą daug anksčiau. 1900–1600 m. pr. m. e babiloniečių lentelėse yra iš esmės aprašyta ta pati teorema.

Viena iš tokių lentelių yra Plimptono molinės lentelės fragmentas 322, kuriame yra atvaizduota Pitagoro trejetų lentelė. Manoma, kad ši lentelė kilo iš Larsos miesto. Lentelėje yra 4 stulpeliai ir 15 eilučių. Ketvirtasis stulpelis iš kairės pusės numeruoja eilutes nuo 1 iki 15. Pirmasis stulpelis yra pažeistas. Antrojo ir trečiojo stulpelio antraštės atitinkamai yra „Plotis“ ir „Įstrižainė“. Pačioje lentelėje yra pateikti skaičiai, kurie naudojami generuoti Pitagoro trejetus:

${\begin{alignedat}{2}(56,90,106)\\(119,120,169)\\(12709,13500,18541)\end{alignedat}}$.

Šie skaičiai rodo, kad babiloniečiai žinojo Diofanto trejetų generavimo metodą.

Kita dantiraščio lentelė yra iš Hamurabio dinastijos (1829–1530 m. pr. m. e.), saugoma Britų muziejuje. Lentelėje yra pateikta geometrinė problema, kurioje reikia apskaičiuoti atstumą, kuriame reikia pastatyti atramą stulpui. Sprendimas pateiktas šešiasdešimtinėje skaičiavimo sistemoje, pritaikant Pitagoro teoremos formulę, kai žinomas vienas trikampio statinis ir įžambinė. Vis dėl to iš šio šaltinio nėra aišku, ar babiloniečiai žinojo patį teoremos matematinį įrodymą.

Remiantis Jamblichu Pitagoras buvo Babilone dvyliką metų.^{[reikalingas šaltinis]}

Kinija

Grafinis trikampio (3, 4, 5) įrodymas, veikale Zhoubi suanjing

V–III a. pr. m. e. kinai jau žinojo, jog trikampis, kurio kraštinių ilgiai lygūs 3, 4 ir 5 (bet kokiais vienetais), yra statusis. Ši teorema yra minima viename iš seniausių kinų matematikos veikalų Zhoubi suanjing. Senovės Kinijos matematinių darbų datavimas yra labai netikslus, o datavimas įvairiuose šaltiniuose labai skiriasi. Zhoubi Suanjing gali siekti 1200 m. pr. m. e., tačiau galutinę formą kūrinys galėjo įgyti kažkada tarp 500 m. pr. m. ir 200 po Kr. Veikale yra astronominių skaičiavimų, taip pat trikampių geometrijos ir šiek tiek apie teorijos apie trupmenas. Kaip ir Babilonijos, Indijos ir Egipto tekstuose, tai yra uždavinių rinkinys su sprendimais. Tarp 246 uždavinių yra trikampio su kraštinėmis 3, 4 ir 5 piešinys (pateiktas dešinėje), iš kurio matosi, jog kinai žinojo teoremą, ją vadina Gougu teorema.

Indija

Indijos tekstuose Baudhayana Shulba Sutra, kurie datuojami įvairiai, maždaug nuo VIII iki V a. pr. m. e., yra Pitagoro trejetų sąrašas ir Pitagoro teoremos teiginys, paminėtas atskiru lygiašonio stačiojo trikampio atveju, taip pat ir bendruoju atveju Apastamba Shulba Sutra tekstuose (apie 600 m. pr. m. e.).

Manoma, kad indai žinių sėmėsi iš Mesopotamijos, tačiau taip pat yra manoma ir atvirkščiai, kad Mesopotamija žinių įgijo iš Indijos.

Įrodymai

Yra žinomi keli šimtai Pitagoro teoremos įrodymų, todėl ji tikriausiai yra labiausiai patikrinta matematinė teorema. 1927 m. amerikiečių matematiko Elisha Scott Loomis pirmą kartą išlestoje knygoje pateiktas 371 įrodymas. Kai kuriuos iš jų pasiūlė Leonardas Da Vinčis ir JAV prezidentas Džeimsas Garfildas.

Įrodymas trikampių panašumu

Iš stačiojo trikampio ABC išvedama aukštinė CH, gaunami du panašūs statieji trikampiai ACH ir CBH.

Vienas iš populiariausių Pitagoro teoremos įrodymų yra įrodymas, kuris remiasi trikampių panašumu, kadangi jis yra beveik tiesiogiai išvedamas iš aksiomų ir nenaudoja figūros ploto koncepcijos.

Šiame įrodyme duodam trikampiui $\triangle ABC$ su stačiuoju kampu $C$ ir kraštinėmis $a,b,c$ bei priešingoms kampams $A,B,C$ išvedama trikampio aukštinė $CH$, gaunami du panašūs statieji trikampiai ir panaudojami trikampių panašumo požymiai: $\triangle ABC\sim \triangle ACH$ ir $\triangle ABC\sim \triangle CBH$, iš kurių seka

${\frac {a}{c}}={\frac {|HB|}{a}},\quad {\frac {b}{c}}={\frac {|AH|}{b}}.$

Tada pasinaudojus pagrindine proporcijos savybe, gaunamos šios lygybės

$a^{2}=c\cdot |HB|,\quad b^{2}=c\cdot |AH|,$

atliekami pertvarkymai ir gaunamas reikalingas rezultatas:

$a^{2}+b^{2}=c\cdot {\big (}|HB|+|AH|{\big )}=c^{2}\quad \Longleftrightarrow \quad a^{2}+b^{2}=c^{2}.$

Įrodymas padalinant kvadratą

Įrodymas padalinant kvadratą

Vienas iš paprastesnių įrodymų yra kvadrato su kraštinėmis $a+b$ padalinimas dviem būdais. Paveikslėlyje kairysis kvadratas sudarytas iš kvadrato su kraštine $a$, kvadrato su kraštine $b$ ir 4 stačiųjų trikampių. Dešinysis kvadratas sudarytas iš kvadrato su kraštine $c$ ir iš tų pačių 4 stačiųjų trikampių.

Abu didieji kvadratai yra vienodo ploto, kadangi jų kraštinės yra lygios: $a+b$. Išėmus 4 stačiuosius trikampis iš abiejų kvadratų, likusios figūros turės vienodą plotą. Kairėje pusėje bus kvadratas su kraštine $a$ ir kvadratas su kraštine $b$, kurie sudarys paviršiaus plotą $a^{2}+b^{2}$. Dešinėje pusėje likęs kvadratas bus su kraštine $c$, tada jo plotas bus $c^{2}$. Pitagoro teorema įrodyta.

Galimas ir trumpesnis šio įrodymo variantas: didžiojo kvadrato su kraštine $a+b$ plotas lygus dešinėje esančio paveikslėlio vidinio kvadrato ir aplink esančių keturių trikampių plotų sumai:

$(a+b)^{2}=c^{2}+4\cdot {\frac {1}{2}}\cdot a\cdot b$

Iš čia

$a^{2}+2ab+b^{2}=2ab+c^{2}\;$

$a^{2}+b^{2}=c^{2}\;$

Algebriniai įrodymai

Dviejų algebrinių įrodymų schema

Pitagoro teorema gali būti įrodyta algebriniu būdu panaudojus 4 vienodus trikampius ir išdėstant juos simetriškai aplinkui kvadratą su kraštine c, kaip pavaizduota šone schemoje apačioje. Taip yra sudaromas didesnis kvadratas, kurio kraštinės yra a + b, o plotas (a + b)². Keturi trikampiai ir kvadrato kraštinė c privalo turėti tą patį plotą kaip ir didysis kvadratas:

$(b+a)^{2}=c^{2}+4{\frac {ab}{2}}=c^{2}+2ab,$

iš to seka

$c^{2}=(b+a)^{2}-2ab=b^{2}+2ab+a^{2}-2ab=a^{2}+b^{2}.$

Panašus įrodymas naudoja 4 stačiuosius trikampius, su kraštinėmis a, b ir c, juos išrikiuojant taip, kad jie būtų kvadrato su kraštine c viduje, kaip pavaizduota šone schemoje viršuje. Šie trikampiai yra panašūs, o jų plotai lygūs ${\tfrac {1}{2}}ab$, susidaręs mažasis kvadratas turi kraštinę b − a ir plotą (b − a)². Didžiojo kvadrato plotas apskaičiuojamas taip:

$(b-a)^{2}+4{\frac {ab}{2}}=(b-a)^{2}+2ab=b^{2}-2ab+a^{2}+2ab=a^{2}+b^{2}.$

Kadangi didysis kvadratas turi kraštinę c ir plotą c²:

$c^{2}=a^{2}+b^{2}.$

Apibendrinimas

Kosinusų teorema

Įprastinis trikampio kraštinių ir kampų žymėjimas.

Stačiajam trikampiu galima pritaikyti kosinusų teoremą:

$c^{2}=a^{2}+b^{2}-2ab\cdot \cos \gamma$,

čia kampas $\gamma$ yra kampas tarp kraštinių $a$ ir $b$. Skirtingai negu Pitagoro, kosinusų teoremoje atsiranda papildomas dėmuo $-2ab\cdot \cos \gamma$. Kadangi $90^{\circ }$ kampo kosinusas yra lygus 0, stačiajam trikampiui šis dėmuo praleidžiamas ir tada kosinusų teorema tampa Pitagoro teorema. Dėl to kartais kosinusų teorema vadinama apibendrintąja Pitagoro teorema.

Skirtumai neeuklidinėse geometrijose

Sferos paviršiuje esančiam tristačiakampiui trikampiui (turi tris 90° kampus) Pitagoro teorema nebetinka.

Neeuklidinėse geometrijose penktasis Euklido postulatas (lygiagretumo postulatas) negalioja. Tokios geometrijos pavyzdys – sferinė geometrija. Šioje geometrijoje trikampis yra sudaromas iš trijų didžiųjų apskritimų lankų, esančių sferoje, kurios spindulys yra $R$. Jeigu du lankai kertasi stačiuoju kampu, Pitagoro teorema nebetinka, kadangi trikampio vidinių kampų suma tampa didesne už 180°. Pitagoro teoremos formulę pakeičiama:

$\cos \left({\frac {c}{R}}\right)=\cos \left({\frac {a}{R}}\right)\cos \left({\frac {b}{R}}\right)$

Panaudojimas

Pitagoro teoremą galima pritaikyti visiems daugiakampiams, nes jie gali būti padalinti į trikampius, o šie į stačiuosius trikampius. Tai galioja ir briaunainiams.

Stačiojo trikampio kraštinių ilgiai

Iš Pitagoro teoremos žinoma, kad stačiojo trikampio įžambinės ilgis yra lygus kvadratinei šakniai iš kitų dviejų kraštinių kvadratų sumos:

$c={\sqrt {a^{2}+b^{2}}}$.

Vadinasi, naudojantis šia teorema galima apskaičiuoti nežinomos kraštinės ilgį žinant įžambinės ir kitos kraštinės ilgius. Pertvarkant gaunamos lygtys:

${\begin{aligned}a&={\sqrt {c^{2}-b^{2}}}\\b&={\sqrt {c^{2}-a^{2}}}\end{aligned}}$

Naudojant atvirkštinę Pitagoro teoremą galima patikrinti, ar duotasis trikampis yra statusis. Tai atliekama tikrinant, ar teoremos lygtis galioja nurodyto trikampio kraštinėms, pavyzdžiui:

• Jeigu trikampio kraštinės $3$, $4$ ir $5$, tada $3^{2}+4^{2}=9+16=25=5^{2}$, vadinasi trikampis statusis.
• Jeigu trikampio kraštinės $4$, $5$ ir $6$, tada $4^{2}+5^{2}=16+25=41\neq 6^{2}$, vadinasi trikampis nėra statusis.

Pitagoro trejetai

Iš visų lygties $a^{2}+b^{2}=c^{2}$ sprendinių $(a,b,c)$, egzistuoja be galo daug tokių $a$, $b$ ir $c$, kurie yra sveikieji skaičiai. Tokios skaičių grupės vadinamos Pitagoro trejetais. Paprasčiausias toks trejetas yra sudarytas iš skaičių $3$, $4$ ir $5$. Pitagoro trejetai buvo nuo senovės laikų naudojami sudarant stačiuosius trikampius.

Pitagoro trejetų paieška skatino ir skaičių teorijos raidą. Prancūzų matematikas Pjeras Ferma studijavo Pitagoro trejetus ir suformulavo Didžiąją Fermą teoremą, kuri teigia, jog lygtis $a^{n}+b^{n}=c^{n}$ neturi sprendinių, kai $n>2$. Šią teoremą po daugiau kaip 300 metų įrodė anglų matematikas Endriu Vailesas.

Euklidinis atstumas

Pitagoro teoremos formulė yra naudojama apskaičiuoti atstumą tarp dviejų taškų Dekarto koordinačių sistemoje. Turint du taškus $(x_{0},y_{0})$ ir $(x_{1},y_{1})$ plokštumoje, atstumas tarpų jų lygus:

$c={\sqrt {(x_{1}-x_{0})^{2}+(y_{1}-y_{0})^{2}}}$

Formulėje remiamasi faktu, jog koordinačių ašys yra statmenos viena kitai. Formulė taip pat gali būti išplėsta ir didesniam matmenų skaičiui, tokiu atveju naudojama sąvoka Euklidinis atstumas, pavyzdžiui, trijų dimensijų Euklidinėje erdvėje:

$c={\sqrt {(x_{1}-x_{0})^{2}+(y_{1}-y_{0})^{2}+(z_{1}-z_{0})^{2}}}$.

Kompleksiniai skaičiai

Kompleksinio skaičiaus $z$ modulis yra atstumas $r$ nuo pradžios taško iki taško $z$ kompleksinėje plokštumoje.

Bet koks kompleksinis skaičius gali būti užrašytas tokia forma:

$z=x+iy.$

Kompleksinio skaičiaus modulis yra apibrėžiamas:

$r=|z|={\sqrt {x^{2}+y^{2}}}.$

Tris dydžius $r$, $x$ ir $y$ jungia Pitagoro teoremos lygtis:

$r^{2}=x^{2}+y^{2}.$

Skaičiaus modulis $r$ yra visada teigiamas, tačiau $x$ ir $y$ abu gali turėti teigiamas arba neigiamas reikšmes. Geometriškai $r$ yra atstumas nuo pradžios taško iki taško $z$ kompleksinėje plokštumoje.

Atstumas tarp dviejų kompleksinių skaičių $z_{1}$ ir $z_{2}$ gali būti apskaičiuojamas:

$|z_{1}-z_{2}|={\sqrt {(x_{1}-x_{2})^{2}+(y_{1}-y_{2})^{2}}}.$

Šis atstumas ir du skaičiai yra susiję per lygtį, kuri yra panaši į Pitagoro teoremos lygtį:

$|z_{1}-z_{2}|^{2}=(x_{1}-x_{2})^{2}+(y_{1}-y_{2})^{2}.$

Trigonometrinis santykis

Vienetiniame apskritime iš Pitagoro teoremos gaunama lygybė $\cos ^{2}\alpha +\sin ^{2}\alpha =1$

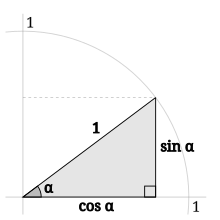
Trigonometrijoje vienetinis apskritimas yra apskritimas, kurio centras yra koordinačių sistemos pradžioje, o spindulio ilgis yra 1. Nubrėžus statųjį trikampį šio apskritimo viduje su įžambine, kuri sutampa su apskritimo spinduliu, prie apskritimo centro susidaro kampas α, kurio kosinusas yra abscisė, o sinusas – ordinatė, tada naudojantis Pitagoro teorema galima užrašyti lygybę:

$\cos ^{2}\alpha +\sin ^{2}\alpha =1$

Literatūra

• Neugebauer, Otto (1969). The exact sciences in antiquity. 9 (Republication of 1957 Brown University Press 2nd leid.). Courier Dover Publications. pp. 1–191. ISBN 0-486-22332-9. OCLC 638685764. PMID 14884919. {{cite book}}: |journal= ignoruotas (pagalba)

Nuorodos

• Eric W. Weisstein, PythagoreanTheorem, MathWorld. (angl.)