Daugiakampis

Daugiãkampis – plokštumos geometrinė figūra, sukuriama plokštumą apribojant baigtiniu tiesių skaičiumi, taip suformuojant uždarą laužtę. Tiesės, sukuriančios daugiakampį, vadinamos daugiakampio kraštinėmis, o taškai, kuriuose šios kraštinės susitinka – daugiakampio viršūnėmis arba kampais. Kartais daugiakampiu yra laikoma ir nepersikertančios laužtės ribojama plokštumos dalis. n-kampis yra daugiakampis, turintis n kraštinių. Daugiakampis yra dvimatis bendrinio politopo pavyzdys.
Dažniausia reikalaujama, kad daugiakampio kraštinės nekirstų viena kitos. Tokie daugiakampiai vadinami paprastaisiais. Daugiakampiai, kurių kraštinės tarpusavyje kertasi, vadinami žvaigždėmis. Geometriškai daugiakampio kraštinės negali susikirsti 180° kampu, nes tokiu atveju atkarpos bus laikomos vienos kraštinės dalimis. Tačiau matematiškai toks kampas įmanomas.
Klasifikacija[redaguoti | redaguoti vikitekstą]
Kraštinių skaičius[redaguoti | redaguoti vikitekstą]
Pirmiausiai daugiakampiai skirstomi pagal kraštinių skaičių (žr. lentelę žemiau).
Vienkampis ir dvikampis paprastai daugiakampiais nelaikomi, nes Euklidinėje erdvėje negalimi. Tačiau šie pavadinimai kartais vartojami grafų teorijoje. Egzistuoja taip pat begalinį kraštinių skaičių turinčio daugiakampio (apeirogono) savoka, reikalinga kai kuriuose fundamentaliose geometrijos užduotyse.
Taisyklingieji daugiakampiai pradedant trikampiu ir baigiant šešiakampiu nubraižomi skriestuvu bei liniuote, nubraižomi ir kai kurie kiti (pavyzdžiui aštuonkampis, septyniolikakampis). Tačiau tarp daugiau kraštinių turinčių daugiakampių vien skriestuvu bei liniuote nubraižomų reta, nors teoriškai įmanoma nubraižyti taisyklingąjį 257-kampį ir 65537-kampį.
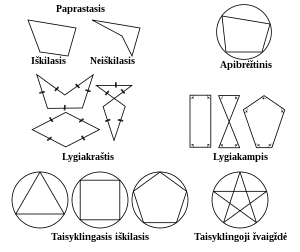
Iškilumas[redaguoti | redaguoti vikitekstą]
Daugiakampiai gali būti skirstomi pagal iškilumą:
- Iškilasis: bet kuri tiesė (išskyrus daugiakampio kraštinės ar kampo liestinė), nubrėžta per daugiakampį, jį kerta lygiai du kartus. Dėl to kiekvienas jo vidinis kampas yra mažesnis nei 180° laipsnių. Taip pat visos daugiakampio įstrižainės yra jo viduje.
- Neiškilasis: egzistuoja bent viena tiesė (išskyrus daugiakampio kraštinės ar kampo liestinė), kuri nubrėžta per daugiakampį, jį kerta daugiau nei du kartus. Taip pat bent viena daugiakampio įstrižainė yra ne jo viduje.
- Paprastasis: daugiakampio kraštinės nekerta viena kitos. Visi iškilieji daugiakampiai yra paprastieji ir atvirkščiai.
- Išgaubtasis: bent vienas vidinis daugiakampio kampas yra didesnis nei 180°.
- Žvaigždinis: visos kraštinės matomos iš vieno vidinio daugiakampio taško, nekertant kraštinių. Šiuo atveju daugiakampis yra paprastasis, tačiau gali būti tiek iškilasis, tiek neiškilasis.
- Žvaigždė: daugiakampis, kurio kraštinės kerta viena kitą tam tikru būdu.
Kitos rūšys[redaguoti | redaguoti vikitekstą]

- Lygiakampis: visi viršūnių kampai lygūs.
- Įbrėžtinis: visi kampai priklauso vienam apskritimui, kuris vadinamas apibrėžtiniu apskritimu.
- Lygiakraštis: visos kraštinės lygios.
- Apibrėžtinis: visos kraštinės yra vieno apskritimo (įbrėžtinio apskritimo) liestinės.
- Taisyklingasis: daugiakampis, kuris yra tiek įbrėžtinis, tiek lygiakraštis. Taigi jis yra ir lygiakampis, ir lygiakraštis. Neiškilasis taisyklingasis daugiakampis vadinamas žvaigžde.
- Monotoniškas tiesei L: kiekviena tiesė, statmena tiesei L, kerta daugiakampį daugiausia du kartus.
- Zonogonas: centro atžvilgiu simetriškas daugiakampis kurio kraštines galima sugrupuoti į lygiagrečias vienodo ilgio, priešingos orientacijos poras.
Savybės[redaguoti | redaguoti vikitekstą]
Toliau aprašoma remiantis euklidine geometrija.
Kampai[redaguoti | redaguoti vikitekstą]
Bet kuris daugiakampis – taisyklingasis, netaisyklingasis, kertantis save, paprastasis – turi tiek pat viršūnių kiek ir kraštinių. Kiekviena viršūnė turi kelis kampus. Patys svarbiausieji yra šie du:
- Vidinis kampas – paprastojo n-kampio vidinių kampų suma yra (n − 2)π radianų arba (n − 2) × 180 laipsnių. Taip yra todėl, kad bet kuris paprastasis n-kampis yra sudarytas iš (n − 2) trikampių, kurio kiekvieno kampų suma yra π radianų, arba 180 laipsnių. Bet kurio iškilojo taisyklingojo n-kampio vidinio kampo dydis yra radianų arba laipsnių.
- Priekampis – kampas, kurį sudaro viena daugiakampio kraštinė ir šalia esančios kraštinės tęsinys. Priekampių suma visada lygi 360°.
Priekampis yra gretutinis kampas vidiniam kampui.
Plotas ir sunkio taškas[redaguoti | redaguoti vikitekstą]
Paprastasis daugiakampis[redaguoti | redaguoti vikitekstą]

Daugiakampio plotas yra daugiakampio apribojamos erdvės dydis. Paprastojo daugiakampio, turinčio n viršūnių, plotas S ir sunkio taškas yra
Tam, kad daugiakampis būtų uždaras, pirmoji ir paskutinė viršūnės turi būti lygios, t. y. xn, yn = x0, y0. Viršūnės turi būti sunumeruotos teigiamąja arba neigiamąja kryptimi (prieš laikrodžio arba pagal laikrodžio rodyklę); jei numeruojama neigiamąja kryptimi, plotas bus neigiamas, tačiau jo modulis teisingas, tačiau, skaičiuojant ir , reikėtų naudoti reikšmę su gautu ženklu (šiuo atveju minusu).
Šios formulės išvedimui reikia paimti kiekvieną daugiakampio kraštinę AB ir apskaičiuoti trikampio ABO su viršūnė O koordinačių pradžios taške plotą (su gautu ženklu) vektorinę sandaugą padalinus iš 2. Aplink daugiakampį „apsukus“ ratą, šie trikampiai su teigiamais ir neigiamais plotais „perdengs“ vienas kitą taip, kad plotas tarp koordinačių pradžios taško ir daugiakampio tampa lygus nuliui ir lieka tik daugiakampio plotas.
Šia formulę 1769 m. aprašė Meisteris, o 1795 m. Gausas. Ją galima įrodyti, daugiakampį padalijus į trikampius. Taip pat šią formulę galima suprasti ir kaip ypatingą Gryno formulės atvejį.
Jei žinomos daugiakampio kraštinės a1, a2, ..., an ir priekampiai θ1, θ2, ..., θn, plotą galima apskaičiuoti ir pagal šią formulę:
Šia formuę 1963 m. aprašė Lopshits.
Jei daugiakampį įmanoma nubraižyti ant langelių taip, kad visos jo viršūnės ir langelių susikirtimo taškuose, galima naudoti daug paprastesnę Piko teoremą.
Kiekvieno daugiakampio, kurio perimetras yra P, o plotas – S, teisinga izoperimterinė nelygybė .
Pagal Valaso-Boljao-Gervino teoremą, jei du daugiakampiai yra vienodo ploto, bet kuris iš jų gali būti padalinamas į mažesnius daugiakampius ir iš tų daugiakampių perstatomas taip, kad būtų gautas antrasis to paties ploto daugiakampis.
Taisyklingojo daugiakampio plotas, jei žinomas į daugiakampį įbrėžtinio apskritimo spindulys r ir daugiakampio perimetras P, yra
Šis spindulys kartais vadinamas apotema.
Jei taisyklingasis n-kampis, kurio kraštinė yra s, yra įbrėžtas į vienetinį apskritimą, tai jo plotas yra
Taisyklingojo n-kampio, kurio apibrėžtinio apskritimo spindulys yra R, o perimetras – P, plotas yra
Taisyklingojo n-kampio, įbrėžto į vienetinį apskritimą, kurio kraštinė yra s, o vidinis kampas – P, plotas yra
Daugiakampio kraštinės nenulemia jo ploto. Tačiau, jei daugiakampis yra įbrėžtinis į apskritimą, tuomet plotas priklauso nuo daugiakampio kraštinių. Iš visų n-kampių dutomis kraštinėmis tas, kurio plotas didžiausias, yra įbrėžtinis į apskritimą. Iš visų n-kampių duotų perimetru tas, kurio plotas didžiausias, yra taisyklingasis (taigi ir įbrėžtinis).
Daugiakampiai, kurių kraštinės kerta viena kitą[redaguoti | redaguoti vikitekstą]
Filosofijoje[redaguoti | redaguoti vikitekstą]
Daug kampų turintys daugiakampiai (daugiausia tūkstantkampis) nuo seno filosofų nagrinėjami priešpastatant vaizduotę ir intelektą.[1] Filosofai teigia jog tūkstantkampio ar kitos panašios figūros neįmanoma įsivaizduoti taip, kaip, pavyzdžiui, galima įsivaizduoti trikampį, jog padrikas tūkstantkampio vaizdinys niekuo nesiskiria nuo kurį vaizduotė pateiktų milijoną kraštinių turinčiam daugiakampiui. Tačiau nagrinėti geometriškai ar matematiškai, nustatyti ploto ir kitokias formules tokioms figūroms visiškai įmanoma, kad ir jų neįsivaizduojant. Taip filosofai grindė požiūrį jog galima nagrinėti bei suprasti ir neįsivaizduojamus dalykus.[1]
Šaltiniai[redaguoti | redaguoti vikitekstą]
- ↑ 1,0 1,1 Sepkoski, David (2005). „Nominalism and constructivism in seventeenth-century mathematical philosophy“. Historia Mathematica. 32: 33–59. doi:10.1016/j.hm.2003.09.002. Nuoroda tikrinta 9 February 2014.









![{\displaystyle {\begin{aligned}S={\frac {1}{2}}(a_{1}[a_{2}\sin(\theta _{1})+a_{3}\sin(\theta _{1}+\theta _{2})+\cdots +a_{n-1}\sin(\theta _{1}+\theta _{2}+\cdots +\theta _{n-2})]\\{}+a_{2}[a_{3}\sin(\theta _{2})+a_{4}\sin(\theta _{2}+\theta _{3})+\cdots +a_{n-1}\sin(\theta _{2}+\cdots +\theta _{n-2})]\\{}+\cdots +a_{n-2}[a_{n-1}\sin(\theta _{n-2})]).\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/f4de84df94bdaccad93c7e9621fc2d632b27a99d)




