Lagero polinomas

Pirmi šeši Lagero polinomai.

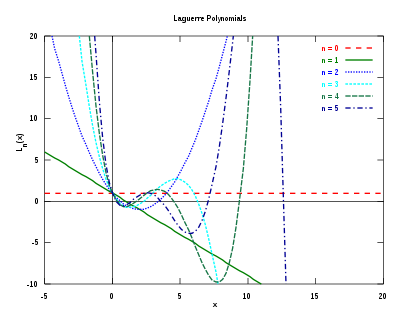
Lagero polinomas (arba Lagero polinomai), pavadintas matematiko Edmondo Lagero (Edmond Laguerre) garbei, – kanoninis antros eilės tiesinės diferencialinės Lagero lygties:

$x\,y''+(1-x)\,y'+n\,y=0\,$

sprendinys.

Ši lygtis turi nesinguliarius sprendinius tik tuomet, kai parametras n yra teigiamas arba lygus nuliui sveikas skaičius.

Šie polinomai dažniausiai yra žymimi $L_{0},L_{1},\dots$ bei sudaro polinomų seka, kurios narius galime apibrėžti kaip:

$L_{n}(x)={\frac {e^{x}}{n!}}{\frac {d^{n}}{dx^{n}}}\left(e^{-x}x^{n}\right).$

Jie priklauso ortogonalių polinomų šeimai, jų vidinė (skaliarinė) sandauga yra apibrėžiama

$\langle f,g\rangle =\int _{0}^{\infty }f(x)g(x)e^{-x}\,dx.$

Lagero polinomai yra svarbūs kvantinėje mechanikoje, kur jie aprašo radialinę Šredingerio lygties sprendinio vienaelektroniam atomui dalį.

Fizikoje Lagero polinomai yra normuojami kitaip negu matematikoje, todėl jie skiriasi nuo apibrėžtų čia per daugiklį $\,(n!)$ (n faktorialas).

Keli pirmi polinomai

Žemiau pateiktos kelių pirmų Lagero polinomų matematinės išraiškos:

n	$L_{n}(x)\,$
0	$1\,$
1	$-x+1\,$
2	${\scriptstyle {\frac {1}{2}}}(x^{2}-4x+2)\,$
3	${\scriptstyle {\frac {1}{6}}}(-x^{3}+9x^{2}-18x+6)\,$
4	${\scriptstyle {\frac {1}{24}}}(x^{4}-16x^{3}+72x^{2}-96x+24)\,$
5	${\scriptstyle {\frac {1}{120}}}(-x^{5}+25x^{4}-200x^{3}+600x^{2}-600x+120)\,$
6	${\scriptstyle {\frac {1}{720}}}(x^{6}-36x^{5}+450x^{4}-2400x^{3}+5400x^{2}-4320x+720)\,$

Taip pat skaitykite

• Gauso pluoštas
• Lagero ir Gauso pluoštas