Gauso funkcija

Matematikoje Gauso funkcija – funkcija, kuri yra apibrėžiama kaip:
Gauso funkcijos grafikas yra būdingas savo simetriniu varpo pavidalu, kuris greitai nuslopsta funkcijos argumento vertėms artėjant į teigiamą arba neigiamą begalybę. Parametras a yra kreivės maksimumo aukštis, dydis b yra maksimumo centro padėtis, o dydis c nulemia "varpo" plotį.
Gauso funkcijos yra plačiai paplitusios įvairiose mokslo srityse – statistikoje, kur jos aprašo normalųjį tikimybės tankio skirstinį, signalų teorijoje, kur jos aprašo Gauso filtrus, vaizdų apdorojime, kur dvimatė Gauso funkcija naudojama "blur" filtro algoritme,[1] bei fizikoje, kur jos yra šilumos pernašos ir parabolinės difrakcijos teorijos diferencialinių lygčių sprendiniai.
Savybės[redaguoti | redaguoti vikitekstą]
Gauso funkcijos yra gaunamos į eksponentinės funkcijos argumentą bet kokį antros eilės polinomą, tokiu būdu, Gauso funkcijos logaritmas visuomet bus kvadratiniu dėsniu aprašoma funkcija.
Signalų teorijoje yra parametras c yra susijęs su pločiu pusiniame aukštyje (angl. "Full Width at Half Maximum", sutr. FWHM) sekančiu sąryšiu
Matematikoje, parametras c gali būti interpretuotas kaip dviejų persilenkimo taškų padėtį nusakantis parametras. Persilenkimo taškai yra ties x = b − c and x = b + c.
Gauso funkcijos yra analitinės, jų riba, kai , yra 0.
Gauso funkcijos priklauso elementarių funkcijų šeimai, tačiau neturi pirminės funkcijos; Gauso funkcijos integralas yra paklaidų funkcija. Nepaisant to, jų apibrėžtas integralas per visą realiųjų skaičių ašį surandamas tiksliai Gauso integralo pagalba
ir po pertvarkimų gaunama
Integralo vertė yra vienetinė tik tuomet, kai a = 1/(c√ (2π)), šiuo atveju Gauso funkcija yra tikimybės tankio funkcija, aprašanti normalųjį skirstinį, žinoma statistikoje. Jis aprašo atsitiktinių dydžių su tikėtina vertė μ = b ir vidutiniu nuokrypiu σ² = c². Gauso funkcijų pavyzdžiai pateikti paveiksliuke
Atlikdami Gauso funkcijos Furjė transformaciją, kuomet a, b = 0 ir c, yra gaunama kita Gauso funkcija su parametrais ac, b = 0 ir 1/c. Tokiu būdu, Gauso funkcijos su b = 0 ir c = 1 nėra iškraipomos Furjė transformacijos (jos yra Furjė transformacijos tikrinės funkcijos, atitinkančios tikrinę vertę 1).
Dviejų Gauso funkcijų sandauga ir sąsuka yra taip pat Gauso funkcija.
Dvimatė Gauso funkcija[redaguoti | redaguoti vikitekstą]
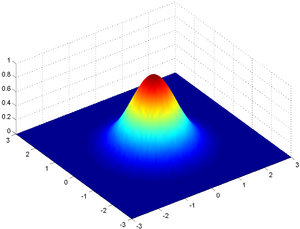
Dalinis dvimatės Gauso funkcijos atvejis yra
Čia dydis A yra amplitudė, xo,yo yra viršunės padėtis ir σx, σy yra pločiai x ir y kryptimis.
Bendru atveju dvimate Gauso funkcija užrašoma taip
kur matrica
yra teigiamai apibrėžta.
Taip pat skaitykite[redaguoti | redaguoti vikitekstą]
Šaltiniai[redaguoti | redaguoti vikitekstą]
- ↑ „Gaussian Blur Algorithm | Pixelstech.net“. pixelstech.net. Nuoroda tikrinta 2024-02-03.








![{\displaystyle \left[{\begin{matrix}a&b\\b&c\end{matrix}}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/74769e46229529b2f5710c4abe3c8906984fe35f)