Įbrėžtinis kampas

Geometrijoje įbrėžtinis kampas – kampas apskritimo viduje, kurio viršūnė yra apskritimo taškas, o kraštinės kerta apskritimą.
Lygiai taip pat įbrėžtinį kampą apibrėžia dvi apskritimo stygos, turinčios vieną bendrą tašką.
Kiekvienas įbrėžtinis kampas, kuris remiasi į apskritimo lanką, iki 180° papildo kitą įbrėžtinį kampą, kuris remiasi į likusį apskritimo lanką.[1]
Įbrėžtinio kampo teorema susieja įbrėžtinio kampo dydį su centriniu kampu, jungiančiu tą patį lanką.
Įbrėžtinio kampo teorema yra 20 teiginys Euklido Pradmenų 3 tome.
Įbrėžtinio kampo teorema
[redaguoti | redaguoti vikitekstą]Teiginys
[redaguoti | redaguoti vikitekstą]
Įbrėžtinio kampo teorema teigia, kad į apskritimą įbrėžtas kampas θ lygus pusei centrinio kampo 2θ, besiremiančio į tą patį lanką. Todėl kampas nesikeičia, kai jo viršūnė perkeliama į skirtingas apskritimo vietas.
Įrodymas
[redaguoti | redaguoti vikitekstą]1. Įbrėžtiniai kampai, kai viena iš stygų yra skersmuo
[redaguoti | redaguoti vikitekstą]
Tegul O yra apskritimo centras, kaip parodyta diagramoje dešinėje. Pasirinkite du apskritimo taškus ir pavadinkite juos V ir A. Nubrėžkite tiesę VO ir pratęskite ją taip, kad ji kirstų apskritimą taške B, kuris būtų vienoje tiesėje su V. Nubrėžkite kampą, kurio viršūnė yra taškas V, o kraštinės eina per taškus A ir B.
Nubrėžkite liniją OA. Kampas BOA yra centrinis kampas, žymime θ. Tiesės OV ir OA yra apskritimo spinduliai, todėl jų ilgis yra vienodas. Vadinasi trikampis VOA yra lygiašonis, todėl kampas BVA (įbrėžtinis kampas) ir kampas VAO yra lygūs. Kiekvienas iš jų žymimas kaip ψ.
Kampai BOA ir AOV sudaro 180°, nes linija VB, einanti per O, yra tiesė. Todėl kampas AOV yra 180° − θ .
Yra žinoma, kad trys trikampio kampai sudaro 180°, tada trys trikampio VOA kampai yra:
- 180° − θ
- ψ
- ψ.
Iš to seka
Atimame iš abiejų pusių
gauname
kur θ yra centrinis kampas, o ψ yra įbrėžtinis kampas.
2. Įbrėžtiniai kampai su apskritimo centru jų viduje
[redaguoti | redaguoti vikitekstą]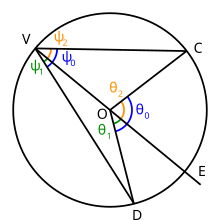
Duotas apskritimas, kurio centras yra taške O, pasirinkite tris apskritimo taškus V, C ir D. Nubrėžkite linijas VC ir VD: kampas DVC yra įbrėžtinis kampas. Dabar nubrėžkite tiesę VO ir pratęskite ją už taško O taip, kad ji kirstų apskritimą taške E. Kampas DVC suformuoja apskritimo lanką DC.
Tarkime, kad šis lankas apima tašką E. Taškas E yra vienoje tiesėje su tašku V. Kampai DVE ir EVC taip pat yra įbrėžtiniai kampai, kadangi abu šie kampai turi vieną kraštinę, kuri eina per apskritimo centrą, todėl jiems galima pritaikyti teoremą iš aukščiau pateikto 1-ojo atvejo.
Todėl,
tada žymime
taip kad
Nubrėžkite linijas OC ir OD. Kampas DOC yra centrinis kampas, kaip ir kampai DOE ir EOC, ir
Žymime
taip kad
Iš 1-ojo atvejo žinome, kad ir . Sujungus šiuos rezultatus su (2) lygtimi, gauname
todėl pagal (1) lygtį
3. Įbrėžtiniai kampai su apskritimo centru jų išorėje
[redaguoti | redaguoti vikitekstą]
Ankstesnis atvejis gali būti išplėstas, kad apimtų atvejį, kai įbrėžtinis kampo dydis yra skirtumas tarp dviejų įbrėžtinių kampų, kaip aptarta 1-ojoje šio įrodymo dalyje.
Duotas apskritimas, kurio centras yra taške O, pasirinkite tris apskritimo taškus V, C ir D. Nubrėžkite linijas VC ir VD: kampas DVC yra įbrėžtinis kampas. Dabar nubrėžkite tiesę VO ir pratęskite ją už taško O taip, kad ji kirstų apskritimą taške E. Kampas DVC suformuoja apskritimo lanką DC.
Tarkime, kad šis lankas neapima taško E. Taškas E yra vienoje tiesėje su V. Kampai EVD ir EVC taip pat yra įbrėžtiniai kampai, kadangi abu šie kampai turi vieną kraštinę, kuri eina per apskritimo centrą, jiems galima pritaikyti teoremą iš aukščiau pateikto 1-ojo atvejo.
Todėl,
- .
tada žymime
taip kad
Nubrėžkite linijas OC ir OD. Kampas DOC yra centrinis kampas, kaip ir kampai EOD ir EOC, ir
Žymime
taip kad
Iš 1-ojo atvejo žinome ir tai . Sujungus šiuos rezultatus su (4) lygtimi, gauname
todėl pagal (3) lygtį,

Išvada
[redaguoti | redaguoti vikitekstą]Pagal panašų teiginį kampas tarp stygos ir liestinės viename iš jos susikirtimo taškų yra lygus pusei centrinio kampo, kurį sudaro styga.
Taikymas
[redaguoti | redaguoti vikitekstą]Įbrėžtinio kampo teorema naudojama daugelyje elementariosios Euklidinės plokštumos geometrijos įrodymų. Atskiras teoremos atvejis yra Talio teorema, kuri teigia, kad kampas, kurį sudaro skersmuo, visada yra 90°, t. y. statusis. Dėl šios teoremos priešingų ciklinių keturkampių kampų suma yra 180°, ir atvirkščiai, bet kuris keturkampis, kuriam tai galioja, gali būti įbrėžtas į apskritimą.
Įbrėžtinių kampų teoremos elipsėms, hiperbolėms ir parabolėms
[redaguoti | redaguoti vikitekstą]Įbrėžtinių kampų teoremos taip pat egzistuoja elipsėms, hiperbolėms ir parabolėms. Esminiai skirtumai yra kampo išmatavimai. (Kampu yra laikoma susikertančių linijų pora.)
Taip pat skaitykite
[redaguoti | redaguoti vikitekstą]Šaltiniai
[redaguoti | redaguoti vikitekstą]- ↑ Hoffmann, Manfred (2007). Didysis matematikos žinynas formulės, taisyklės, teoremos, uždaviniai ir jų sprendimai. Kaunas. p. 217. ISBN 5-430-04814-3. OCLC 1185091387.
{{cite book}}: CS1 priežiūra: location missing publisher (link)
Literatūra
[redaguoti | redaguoti vikitekstą]- Ogilvy, C. S. (1990). Excursions in Geometry. Dover. pp. 17–23. ISBN 0-486-26530-7.
- Gellert W, Küstner H, Hellwich M, Kästner H (1977). The VNR Concise Encyclopedia of Mathematics. New York: Van Nostrand Reinhold. pp. 172. ISBN 0-442-22646-2.
- Moise, Edwin E. (1974). Elementary Geometry from an Advanced Standpoint (2nd leid.). Reading: Addison-Wesley. pp. 192–197. ISBN 0-201-04793-4.
Nuorodos
[redaguoti | redaguoti vikitekstą]- Eric W. Weisstein, Inscribed Angle, MathWorld. (angl.)
- Relationship Between Central Angle and Inscribed Angle (angl.)
- Munching on Inscribed Angles (angl.)
- Arc Central Angle (angl.)
- Arc Peripheral (inscribed) Angle (angl.)
- Arc Central Angle Theorem (angl.)
- At bookofproofs.github.io Archyvuota kopija 2023-02-01 iš Wayback Machine projekto. (angl.)


























