Kūgio pjūvis

Kūgio pjūviai

Kūgio pjūviai – plokštumos kreivės, gaunamos kūgį sukertant su plokštuma. Kūgio pjūviai įvardinti ir nagrinėti jau 200 m. pr. m. e., kai Apolonijas Pergietis sistemiškai tyrė jų savybes.

Geriausiai žinomi kūgio pjūviai – apskritimas ir elipsė, gaunami, kai plokštumos ir kūgio sankirta sudaro uždaras kreives. Apskritimas – atskiras elipsės atvejis, kai kūgį kertanti plokštuma yra statmena kūgio ašiai. Jei plokštuma yra lygiagreti kūgį generuojančiai tiesei, gaunama kreivė vadinama parabole. Kitais atvejais, kai gaunama atvira kreivė, bet plokštuma nelygiagreti generuojančiai kraštinei, gaunama hiperbolė. Šiuo atveju plokštuma kerta abi kūgio puses, todėl gaunasi dvi atskiros kreivės, bet paprastai viena iš jų pamirštama.

Kūgį kertant plokštumomis einančiomis per jo sudaromąsias gaunami trikampiai, jeigu tokia plokštuma dar ir kerta kūgio ašį, ji vadinama ašiniu pjūviu. Ašinis pjūvis yra lygiašonis trikampis, kurio pagrindas yra kūgio pagrindo skersmuo, o šoninės kraštinės - kūgio sudaromosios. Likę pjūvių atvejai, kai sankirtą sudaro taškas ar tiesė, laikomi iškreiptais ir dažnai nelaikomi kūgio pjūviais.

Kūgio pjūvių lygtys

Kūgio pjūvius galima apibūdinti Dekarto koordinačių sistemoje antrojo laipsnio lygtimis:

Elipsė

Parabolė

Hyperbolė

• Elipsė, kurios centras M yra taške (0,0), o pagrindinė ašis yra x ašyje:

  ${\frac {x^{2}}{a^{2}}}+{\frac {y^{2}}{b^{2}}}=1,\quad b=|MS_{3}|,\qquad a,b\neq 0\quad$

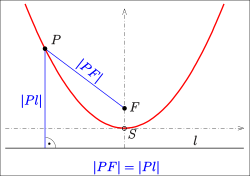
• Parabolė, kurios viršūnė yra taške (0,0), o ašis yra y ašyje:

  $y=ax^{2},\quad a={\frac {1}{4|SF|}},\qquad a\neq 0\quad ,$

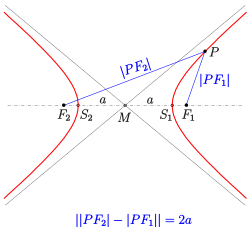
• Hiperbolė, kurios centras M yra taške (0,0), o pagrindinė ašis yra x ašyje:

  $y=ax^{2},\quad a={\frac {1}{4|SF|}},\qquad a\neq 0\quad$

Taikymas

Kūgio pjūviai yra svarbūs astronomijoje, kur dviejų gravitacijos jėgų veikiamų masyvių kūnų orbitos yra kūgio pjūviai masės centrus laikant nekintamais. Jei kūnai susiję, jie juda elipsine orbita, jei nesusiję – parabole ar hiperbole.