Apibrėžtinis integralas
Matematikoje apibrėžtiniu integralu vadinamas įrankis, skirtas skaičiuoti adityviems dydžiams, pvz., plotui, masei ir t. t.
Šiuolaikinę apibrėžtinio integralo sąvoką įvedė prancūzų matematikas Ogiustenas Luji Koši.[1]
Egzistuoja keletas apibrėžtinio integralo apibrėžimų:
ir t. t. Praktikoje dažniausiai naudojamas Rymano integralas. Visi apibrėžimai yra panašūs ir integralų prasmės iš esmės tos pačios, skiriasi formuluotės.
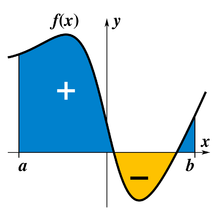
Šių integralų esmę galima įsivaizduoti taip: turime intervalą , skaidome jį į be galo mažus gabaliukus. Kiekvienas toks gabaliukas susietas su kažkokiu skaičiumi (apibrėžta funkcija šiame intervale). Dauginame kiekvieno gabaliuko ilgį iš to skaičiaus ir viską susumuojame. Riba, kai tokio gabaliuko ilgis be galo mažas ir yra vadinama apibrėžtiniu integralu.
Naudojami ir kitaip apibrėžti integralai:
- Kai intervalas yra ne tiesė, o kažkokia kreivė, kurios lygtį žinome, tai integralas vadinamas kreiviniu. Jis naudojamas, kai, pvz., taškas juda kažkokia kreive jėgų lauke ir norime rasti jėgų lauko atliką darbą.
- Integralas, kai turime kažkokį paviršių ir skaidome jį į mažus plotelius, dauginame juos iš tam tikros vertės ir sumuojame, vadinamas paviršiniu integralu. Taikome, pvz., kai norime rasti ant paviršiaus sukauptą elektros krūvį, kai žinome jo pasiskirstymą.
- Integralai, kai vietoj intervalo naudojame n matavimų sritį, su kurios kiekvienu gabaliuku susietas skaičius (pvz., dvimatė funkcija, apibrėžta stačiakampyje), vadinami n-lypiais integralais. Pvz., kai naudojame plokščią dvimatę sritį, turime dvilypį integralą. Jo geometrinė prasmė – tūris po paviršiumi. Kai sumuojame trimatės srities gabaliukus – turime trilypį integralą. Jo geometrinė prasmė – tūris keturmatėje erdvėje. Tačiau jis taikomas praktikoje, pvz., kūno kiekviename taške apibrėžtas jo tankis. Sumuodami gabaliuko tūrius, padaugintus iš tankio tose vietose, gausime kūno masę.
Taip pat skaitykite[redaguoti | redaguoti vikitekstą]
- Neapibrėžtinis integralas
- Dvilypis integralas
- Trilypis integralas
- Kreiviniai integralai
- Gryno formulė
Šaltiniai[redaguoti | redaguoti vikitekstą]
- ↑ Autorių kolektyvas. Matematika. Mokomoji knyga XII klasei ir gimnazijų IV klasei I dalis. – Kaunas: Šviesa, 2003. – 78 p. ISBN 5-430-03746- X

![{\displaystyle [a;b]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/68e776d74130a8890a814c1f4e74372a9110d2f9)