Taisyklingas dodekaedras
Išvaizda
| Taisyklingas dodekaedras | |
|---|---|
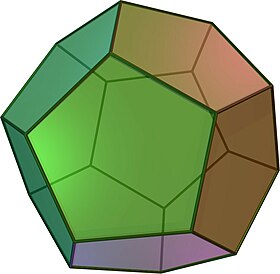 (Čia spustelėjus, suksis) | |
| Tipas | Platono kūnas |
| Elementai | F = 12, E = 30 V = 20 (χ = 2) |
| Sienos pagal puses | 12{5} |
| Konvėjaus užrašas | D gT |
| Šlėfli simbolis | {5,3} |
| Vithofo simbolis | 3 | 2 5 |
| Kokseterio diagrama | |
| Simetrija | Ih, H3, [5,3], (*532) |
| Sukinio grupė | I, [5,3]+, (532) |
| Indeksai | U23, C26, W5 |
| Savybės | taisyklingas iškilas |
| Dvisienis kampas | 116.56505° = arccos(-1/√5) |
 5.5.5 (Viršūnės planas) |
 Taisyklingas ikosaedras (dualus briaunainis) |
 Išklotinė | |
Taisyklingas dodekaedras arba penkiakampis dodekaedras – dodekaedras, sudarytas iš dvylikos taisyklingų penkiakampių sienų, kurios po tris sueina į kiekvieną viršūnę, o jo sandarą aprašo Schläfli simbolis {5,3}. Tai vienas penkių Platono kūnų. Jis turi 20 viršūnių, 30 briaunų ir 160 įstrižainių (60 sienose ir 100 vidaus erdvėje),[1] o prie kiekvienos viršūnės esančių plokščiųjų kampų suma lygi 324°.[2]
Euklidas sukonstravo taisyklingąjį dodekaedrą ant kubo briaunų.[3] Papas Aleksandrietis įrodė, kad taisyklingojo dodekaedro viršūnės po penkias priklauso keturioms lygiagrečioms plokštumoms, sudarant kiekvienoje iš jų taisyklingąjį penkiakampį.

Išnašos
[redaguoti | redaguoti vikitekstą]- ↑ Sutton, Daud (2002), Platonic & Archimedean Solids, Wooden Books, Bloomsbury Publishing USA, p. 55, ISBN 9780802713865
- ↑ Vaidotas Mockus. Geometrijos žinynas moksleiviams. – Šiauliai: Šiaulių pedagoginis institutas, 1996. – 142 p. ISBN 9986-38-010-3
- ↑ Euklid's Elements. Book XIII. Proposition 17
