Keturkampis

Keturkampis – geometrinė figūra, sudaryta iš keturių taškų ir keturių nuosekliai juos jungiančių atkarpų. Bet kurie trys iš tų taškų negali būti išsidėstę vienoje tiesėje, o juos jungiančios atkarpos negali kirstis. Tuos keturis taškus vadiname keturkampio viršūnėmis, o juos jungiančias atkarpas – keturkampio kraštinėmis.[1]
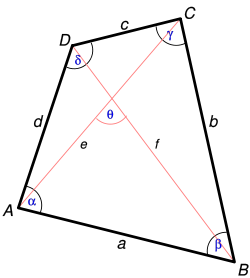
Keturkampis žymimas keturiomis didžiosiomis raidėmis, savo viršūnių pavadinimais (pavyzdžiui, 1 pav. pavaizduotas keturkampis ABCD).
Keturkampio viršūnės, priklausančios tai pačiai kraštinei, vadinamos gretimomis viršūnėmis, o viršūnės, nepriklausančios tai pačiai kraštinei, vadinamos priešingomis viršūnėmis. Keturkampio kraštinės, išeinančios iš tos pačios viršūnės, vadinamos gretimomis kraštinėmis, o kraštinės, neturinčios bendros viršūnės, vadinamos priešingomis kraštinėmis.
Keturkampis turi keturis vidinius kampus, kurių suma lygi 360°:[2]
Atkarpos, jungiančios priešingas keturkampio viršūnes, vadinamos keturkampio įstrižainėmis. Visi keturkampiai turi dvi įstrižaines. (1 pav. pavaizduoto keturkampio įstrižainės yra AC ir BD.)
Keturkampio apribota plokštumos dalis vadinama keturkampio vidumi, o kita dalis – keturkampio išore.
Keturkampiai yra skirstomi į iškiliuosius ir neiškiliuosius. Keturkampiai, kurių abi įstrižainės yra keturkampių viduje, yra iškilieji. Neiškilieji keturkampiai šia savybe nepasižymi.
Geometrijoje dažniau nagrinėjami iškilieji keturkampiai. Pastarieji dar yra skirstomi į lygiagretinius, trapecijas.
- Jei a, b, c ir d yra kraštinės betkokio keturkampio, o ir – keturkampio įstrižainės, tai
- čia m yra ilgis tiesės jungiančios keturkampio įžambinių vidurio taškus.
Plotas į apskritimą įbrėžto keturkampio su kraštinėmis a, b, c, d yra lygus (įbrėžti keturkampį galima, kai jo priešingų kampų suma lygi 180 laipsnių):
- čia
Plotas bet kokio iškilojo keturkampio lygus:
- čia ir yra keturkampio įstrižainės, o yra smailus kampas tarp keturkampio įstrižainių.
Apibrėžimas[redaguoti | redaguoti vikitekstą]

Tegul , , ir yra keturi taškai vienoje plokštumoje ir trys iš jų nėra vienoje tiesėje. Jeigu atkarpos , , ir susikerta tik galiniuose taškuose, tai šių atkarpų susikirtimas yra keturkampis, kurį galima apibūdinti taip:
keturkampis yra atkarpų sąjunga (žr. 2 pav.).
Keturkampio elementai[redaguoti | redaguoti vikitekstą]
Keturkampio elementai yra:
- 4 viršūnės: kraštinių, sudarančių keturkampį, susikirtimo taškai.
- 4 kraštinės: atkarpos, jungiančios gretimas viršūnes.
- 2 įstrižainės: atkarpos, kurių galiniai taškai yra dvi negretimos viršūnės.
- 4 vidiniai kampai: kampai, kuriuos sudaro dvi gretimos kraštinės.
- centras, kuris yra į keturkampį įbrėžto apskritimo centras.
Keturkampio savybės[redaguoti | redaguoti vikitekstą]
- Visų keturkampių vidinių kampų suma yra 360 laipsnių.
- Visi keturkampiai turi dvi įstrižaines.
- Keturkampis yra arba išgaubtas, arba įgaubtas.
- Išgaubto keturkampio įstrižainės susikerta viename taške, bet įgaubto keturkampio įstrižainės – ne.
- Bet kokį keturkampį galima nubrėžti tada, kai žinomi 5 jo elementai (kraštinės arba kampai).[3]
Įbrėžtinis ir apibrėžtinis apskritimas[redaguoti | redaguoti vikitekstą]

Į keturkampį galima įbrėžti apskritimą tik tada, kai keturkampio priešingų kraštinių ilgių sumos yra lygios: , kur kraštinė a yra priešais kraštinę c ir kraštinė b yra priešais kraštinę d.
Keturkampį galima apibrėžti apskritimu tada ir tik tada, kai priešingų vidinių kampų suma yra 180°:[4] , kur kampas yra priešais kampą , o kampas yra priešais kampą
Klasifikacija[redaguoti | redaguoti vikitekstą]
Keturkampiai yra klasifikuojami pagal jų kraštinių lygiagretumą, ilgį ir vidinius kampus:
- trapecija – dvi priešingos kraštinės yra lygiagrečios.
- lygiašonė trapecija – du trapecijos pagrindai yra lygiagretūs, šoninės kraštinės yra vienodo ilgio ir trapecijos kampai prie kiekvieno iš pagrindų yra lygūs. Tai reiškia, kad įstrižainės yra vienodo ilgio.
- lygiagretainis – priešingosios kraštinės yra lygiagrečios. Iš to seka, kad priešingosios kraštinės yra lygios, priešingieji kampai yra lygūs ir įstrižainės susikerta ir susikirtimo taškas jas dalija pusiau.
- deltoidas – dvi gretimos kraštinės yra vienodo ilgio, kaip ir dvi kitos. Tai reiškia, kad ta priešingų kampų aibė yra lygi, o ta įstrižainė dalija kitą stačiu kampu.
- romboidas – lygiagretainis, kurio gretimos kraštinės yra nevienodo ilgio, o du kampai yra didesni už kitus du.
- stačiakampis – visi keturi kampai yra statieji. Tai reiškia, kad priešingos kraštinės yra lygiagrečios ir lygios, o įstrižainės susikerta ir susikirtimo taškas dalija jas į vienodas dalis.
- kvadratas – taisyklingasis keturkampis, kurio visos kraštinės yra lygios ir visi vidiniai kampai yra statūs. Tai reiškia, kad priešingos kraštinės yra lygiagrečios ir lygios, o įstrižainės susikerta stačiu kampu ir susikirtimo taškas dalija jas į vienodas dalis. Keturkampis yra kvadratas tada ir tik tada, kai jis yra ir rombas, ir stačiakampis.
- įbrėžtinis keturkampis: keturios viršūnės yra apibrėžtiniame apskritime.
Formulės[redaguoti | redaguoti vikitekstą]
| Bendrinio keturkampio matematinės formulės | ||
|---|---|---|
| Plotas | ||
| Įstrižainės ilgis
(žr. kosinusų teorema) |
||
| Vidinis kampas
(žr. kosinusų teorema) |
||
Šaltiniai[redaguoti | redaguoti vikitekstą]
- ↑ Vaidotas Mockus. Geometrijos žinynas moksleiviams. – Šiauliai: Šiaulių pedagoginis institutas, 1996. – 63 p. ISBN 9986-38-010-3
- ↑ „Quadrilaterals - Square, Rectangle, Rhombus, Trapezoid, Parallelogram“. mathsisfun.com (anglų). Nuoroda tikrinta 2023-02-25.
- ↑ Hoffmann, Manfred (2007). Didysis matematikos žinynas formulės, taisyklės, teoremos, uždaviniai ir jų sprendimai. Kaunas. p. 208. ISBN 5-430-04814-3. OCLC 1185091387.
{{cite book}}: CS1 priežiūra: location missing publisher (link) - ↑ Birutė Gražulevičienė. Mokyklinės matematikos žinynas. – Vilnius: Leidybos centras, 1997. – 84 p. ISBN 9986-03-264-4
Nuorodos[redaguoti | redaguoti vikitekstą]
- Eric W. Weisstein, Quadrilateral, MathWorld. (angl.)