Apskritimo ilgis

Geometrijoje apskritimo ilgis – apskritimo perimetras.^[1] Dar gali būti apibrėžtas, kaip visas ištiesinto apskritimo iki tiesės ilgis.^[2]

Žymimas raide C, pagal lotynų kalbos žodį circumferens, reiškiantį „nešioti aplinkui“.

Ryšys su π[redaguoti | redaguoti vikitekstą]

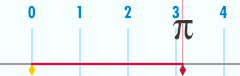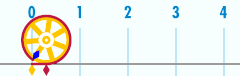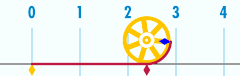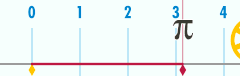
Kai apskritimo skersmuo yra 1, jo apskritimo ilgis yra lygus $\pi .$

Kai apskritimo spindulys yra 1, toks apskritimas yra vadinamas vienetiniu apskritimu, jo apskritimo ilgis yra $2\pi .$

Apskritimo ilgis yra susijęs su viena iš svarbiausių matematinių konstantų. Ši konstanta pi yra žymima graikiška raide $\pi .$ Pirmieji keli skaičiaus $\pi$ skaitmenys yra 3,141592653589793… Pi apibrėžiamas kaip apskritimo perimetro $C$ santykis su jo skersmeniu $d:$

\pi ={\frac {C}{d}}.

Arba, dar kaip apskritimo ir dvigubo spindulio santykis. Aukščiau pateiktą formulę galima pertvarkyti ir išsireikšti apskritimo ilgį:

{C}=\pi \cdot {d}=2\pi \cdot {r}.\!

Matematinė konstanta π naudojama visur matematikoje, inžinerijoje ir moksle.

Traktate „Apskritimo matavimas“, parašytame maždaug 250 m. pr. m. e., Archimedas apskaičiuodamas įbrėžtinio ir apibrėžtojo taisyklingojo 96 kraštinių daugiakampio perimetrus parodė, kad šis $C/d,$ santykis (jis nevartojo termino π) buvo didesnis nei 310/71, bet mažesnis negu 31/7.^[3] Toks π aproksimavimo metodas buvo naudotas šimtmečius, o siekiant didesnio tikslumo buvo imami vis didesnio kraštinių skaičiaus daugiakampiai. Paskutinį kartą tokį skaičiavimą 1630 m. atliko Kristupas Grynbergeris, naudojęs 10⁴⁰ kraštinių daugiakampius.

Šaltiniai[redaguoti | redaguoti vikitekstą]

↑ San Diego State University (2004). „Perimeter, Area and Circumference“ (PDF). Addison-Wesley. Suarchyvuotas originalas (PDF) 2014-10-06.
↑ Bennett, Jeffrey & Briggs, William (2005), Using and Understanding Mathematics / A Quantitative Reasoning Approach (3rd ed.), Addison-Wesley, p. 580, ISBN 978-0-321-22773-7
↑ Katz, Victor J. (1998), A History of Mathematics / An Introduction (2nd ed.), Addison-Wesley Longman, p. 109, ISBN 978-0-321-01618-8

[1] San Diego State University (2004). „Perimeter, Area and Circumference“ (PDF). Addison-Wesley. Suarchyvuotas originalas (PDF) 2014-10-06.

[2] Bennett, Jeffrey & Briggs, William (2005), Using and Understanding Mathematics / A Quantitative Reasoning Approach (3rd ed.), Addison-Wesley, p. 580, ISBN 978-0-321-22773-7

[3] Katz, Victor J. (1998), A History of Mathematics / An Introduction (2nd ed.), Addison-Wesley Longman, p. 109, ISBN 978-0-321-01618-8

[1]

[2]

[3]