Hablo dėsnis

Hablo dėsnis teigia, kad galaktikų tolimo greitis v yra proporcingas jų nuotoliui R nuo stebėtojo. Tyrinėjant galaktikų spektrus buvo surastas raudonasis poslinkis - tai reiškia, jog galaktikos dideliu greičiu tolsta nuo mūsų, taigi Visata plečiasi. Po beveik dešimtmetį trukusių tyrinėjimų 1929 metais dėsnį pirmieji suformulavo Edvinas Hablas ir Miltonas Humansonas:

$v=H\cdot R,$

čia

H - Hablo konstanta.

Stebėjimais pagrįstas Hablo dėsnis padėjo pamatus besiplečiančio kosmoso paradigmai ir šiandien yra vienas iš labiausiai cituojamų darbų Didžiojo sprogimo teorijai patvirtinti. Naujausi Hablo konstantos skaičiavimai naudojant WMAP palydovą prasidėjo 2003 metais, nustatyta konstantos vertė yra 71 ± 4 (km/s)/Mpc. 2006 metų rugpjūtį orbitinėje Chandra X-ray observatorijoje NASA gavo Hablo konstantą kiek mažesniu tikslumu – 77 (km/s)/Mpc su ± 15 % paklaida.

Iš Hablo dėsnio išplaukia, kad bet kurioje vietoje esančiam stebėtojui atrodo, jog visos galaktikos tolsta nuo jo į visas puses nevienodais greičiais: kuo toliau galaktika, tuo jos greitis didesnis. Dabar žinomos galaktikos, kurių tolimo greitis siekia 97% šviesos greičio.

Plėtimosi pradžia

Jei visata plečiasi tam tikru greičiu ir nuotoliai tarp galaktikų didėja, tai pagal Hablo dėsnį galima apskaičiuoti ir to plėtimosi pradžią – maždaug prieš 13 milijardų metų. Manoma, kad tada įvyko Didysis sprogimas – Visata susidarė iš milžiniškos masės ir labai didelio tankio kūno, kuris sprogo dėl nežinomos priežasties.

Atradimas

Dar prieš Hablo tyrinėjimus, naudodamiesi Einšteino lauko lygtimis ir bendrąja reliatyvumo teorija, daugybė fizikų ir matematikų buvo įvedę neprieštaringą erdvės ir laiko priklausomybės teoriją. Bendriausiųjų principų taikymas tyrinėjant Visatos prigimtį leido kalbėti apie dinamišką, o ne statišką Visatą, kas prieštaravo tuo metu vyraujančiam požiūriui.

1922 metais Aleksandras Frydmanas iš Einšteino lauko lygčių išvedė Frydmano lygtis, kuriomis apskaičiuojamas galimas Visatos plėtimosi koeficientas. Frydmano naudotas parametras, šiandien žinomas kaip mastelio daugiklis, gali būti suprantamas kaip Hablo dėsnio proporcingumo konstantos forma. 1927 metais Georges Lemaître taip pat atrado panašų šios problemos sprendimą. Frydmano lygtims išvesti prireikė į skysčiams skirtas Einšteino lauko lygtis, kai žinomas tankis ir slėgis, įvesti homogeniškos ir izotropinės Visatos metriką (tam tikra atstumo sąvoka). Besiplečiančio erdvėlaikio idėja atvedė prie kosmologinių Didžiojo sprogimo ir Rimties būvio teorijų. Apie Visatos dydį ir formą buvo daug kalbų dar prieš šiuolaikinės kosmologijos atsiradimą. 1920 metais šiuo klausimu vyko garsusis Shapley-Curtis ginčas tarp Harlow Shapley ir Hebero D. Curtiso. Shapley teigė, kad Visata yra Paukščių tako dydžio, o Curtisas – kad ji kur kas didesnė.

Nepraėjus nė dešimčiai metų šį nesutarimą išsprenė Hablo atlikti stebėjimai. Didžiąją dalį profesionalių astronominių stebėjimų Edvinas Hablas atliko Mount Wilsono observatorijoje, kur buvo laikomas galingiausiais tų laikų teleskopas. Spiralinių ūkų cefeidžių stebėjimai leido Hablui apskaičiuoti jų nuotolį. Pasirodė, kad šie objektai yra už Paukščių tako ribų. Pradžioje šie ūkai buvo vadinami „Visatos salomis“ ir tik vėliau imti vadinti galaktikomis.

Lygindamas galaktikų nuotolio skaičiavimus su Vesto Sliferio galaktikų raudonųjų poslinkių skaičiavimais, Hablas atrado apytikrį objektų nuotolio proporcingumą. Net ir susidūręs su didele sklaida (dabar žinoma kaip pekuliarieji greičiai), Hablas sugebėjo pagal 46 jau ištirtų galaktikų duomenis išvesti tam tikrą tendenciją ir apibrėžti Hablo konstantos vertę – 500 km/s/Mpc, kuri dėl atstumų kalibracijos klaidų buvo žymiai didesnė nei dabar priimtoji. 1958 metais Allan Sandage išplatino pirmąjį tiksliai apskaičiuotą H₀ – 75 km/s/Mpc, tačiau prireikė dar kelių dešimtmečių, kad būtų pasiektas galutinis susitarimas.

Po to, kai buvo paskelbtas Hablo atradimas, Albertas Einšteinas iš savo darbų eliminavo kosmologinę konstantą, kurią buvo sukūręs tam, kad gautų pastovius lygčių sprendinius. Vėliau Einšteinas pavadino kosmologinę konstantą „apmaudžia klaida“, nes, pasak jo, tikėjimas Visatos statiškumu užkirto kelią besiplečiančios Visatos pažinimui. 1931 metais Einšteinas nuvyko į Mount Vilsoną padėkoti Hablui už šiuolaikinės kosmologijos pagrindus.

Aiškinimas

Tiesinės priklausomybės tarp raudonojo poslinkio, arba objekto tolimo greičio, ir jo nuotolio atradimas veda prie tokios Hablo dėsnio matematinės išraiškos:

$v=H_{0}\,D$

kur $v$ yra tolimo greitis išreikštas km/s. H₀ yra Hablo konstanta, Frydmano lygtyse (kur stebėjimo laikas žymimas apatiniu indeksu 0) atitinkanti H – nuo laiko priklausomą Hablo parametrą. Ši reikšmė surištame su stebėtoju laike yra bendra visai Visatai. D yra atstumas tarp galaktikos ir stebėtojo, matuojamas megaparsekais (Mpc), ir trimatėje erdvėje nusakomas kosmologiniu laiku. Tolimo greitis lygus v = dD/dt.

Kaip matyti iš formulės, tiriant labai nutoliusius objektus, v gali būti didesnis už c. Tačiau tai neprieštarauja specialiajai reliatyvumo teorijai, nes jos taikymas dviem labai nutolusioms galaktikoms būtų iš esmės klaidingas. Specialioji reliatyvumo teorija tvirtina, kad joks objektas negali judėti kito atžvilgiu didesniu už šviesą greičiu, tačiau neteigia, kad už šviesą didesnio greičio būti negali.

D ir v negali būti tiesiogiai stebimi, nes nurodo galaktikos dabartį, o stebint iš tiesų matoma galaktikos praeitis – momentas, kai mus pasiekianti šviesa paliko stebimą galaktiką. Artimesnėms galaktikoms, kurių raudonasis poslinkis z yra mažesnis už vienetą, o v ir D mažai pakitę, galima taikyti formulę v = zc, kur z - raudonasis poslinkis, c – šviesos greitis. Tai ir yra Hablo atrastas empirinis ryšys. Žinant tolimųjų galaktikų z negalima apskaičiuoti v (arba D), nenurodžius tikslaus H kitimo laike. Raudonasis poslinkis tiesiogiai yra susijęs ne tik su objekto, išspinduliavusio šviesą pradiniu tolimo greičiu, bet turi ir kitą paaiškinimą: (1+z) yra dydis kuris nusako kiek Visata išsiplėtė kol fotonas keliavo iki stebėtojo.

Pagal Hablo dėsnį skaičiuojant atstumus, gali būti naudojamas tik greitis, nes Visata nuolat plečiasi. Kadangi gravitaciškai saveikaujančios galaktikos viena kitos atžvilgiu juda nepriklausomai nuo Visatos plėtimosi, taikant Hablo dėsnį būtina atsižvelgti į šiuos santykinius greičius (tai vadinamieji "pekuliarieji greičiai" - 1938 metais Benjamin Kenneally atrasto "Dievo piršto" efektas). Gravitacijos ribojamose sistemose, kaip galaktikos ar mūsų planetų sistema, erdvės plėtimąsi stabdo traukos jėga.

Visatos amžių ir likimą galima nusakyti dabartinę Hablo konstantą ekstrapoliuojant su apskaičiuota lėtėjimo parametro reikšme, nusakoma tankio parametrais(Ω). Vadinamosios uždarosios Visatos (Ω>1) gyvavimas baigiasi Didžiaja krize; tokia Visata yra žymiai jaunesnė nei rodo jos Hablo amžius. Tuo tarpu atviroji Visata (Ω≤1) amžinai plečiasi ir jos amžius yra artimesnis Hablo amžiui. Taip jau sutapo, kad mūsų greitėjančios Visatos amžius yra labai artimas Hablo nustatytajam.

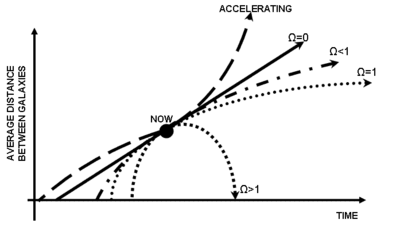
Hablo parametro reikšmė su laiku kinta – didėja ar mažėja priklausomai nuo lėtėjimo parametro q, kuris apibrėžiamas taip:

$q=-H^{-2}\left({{\;dH} \over {\;dt}}+H^{2}\right)$

Kai Visatos lėtėjimo parametras q lygus nuliui – H = 1/t, kur t yra laikas, praėjęs po Didžiojo sprogimo. Nelygus nuliui ir nuo laiko priklausantis parametras q reikalauja Friedmann'o lygčių integravimo laiku.

Ilgai buvo manoma, kad q reikšmė yra teigiama, iš ko išplaukia, kad Visata dėl gravitacinės traukos plečiasi lėčiau. Tai reikštų, kad Visatos amžius yra mažesnis, nei 1/H, arba apytikriai 14 mln. metų. Pavyzdžiui, jei q lygus 1/2, kaip kadaise manė dauguma teoretikų, Visatos amžius yra 2/(3H). 1998 metų atradimas, kad q yra akivaizdžiai neigiamas, reiškia, kad Visata gali būti senesnė nei 1/H. Bandymai nustatyti Visatos amžių labai artimi 1/H reikšmei.

Olberso paradoksas

Hablo dėsnio Didžiojo sprogimo interpretacija apibendrino kosmoso plėtimosi idėją, kuri yra susijusi su senu kosmologijos galvosūkiu – Olberso paradoksu: jei Visata būtų begalinė, statiška ir žvaigždės joje būtų pasiskirsčiusios tolygiai (iš viso to išplaukia, kad žvaigždžių skaičius turi taip pat būti begalinis), tai kiekvieno į dangų nukreiptas žvilgsnis turėtų susidurti su žvaigžde ir dangus būtų toks pat šviesus, kaip ir žvaigždžių paviršius. Tačiau nakties dangus yra tamsus. Nuo pat XVII a. astronomai ir kiti mąstytojai pasiūlė daugybę galimų šio paradokso aiškinimų, bet dabartinis visuotinai priimtas požiūris bent iš dalies priklauso nuo Didžiojo sprogimo teorijos ir Hablo dėsnio. Ribotą laiką gyvuojančioje Visatoje mus pasiekė tik riboto žvaigždžių skaičiaus šviesa, tokiu atveju paradoksas išspręstas. Be to, nuolat besiplečiančioje Visatoje tolimi objektai nuo mūsų traukiasi ir todėl jų spinduliuojamoje šviesoje vyksta raudonasis poslinkis ir ji slopsta. Prie Olberso paradokso prisideda abu minėtieji veiksniai, tačiau prisiminus, kad pardoksas formuluojamas statiškai Visatai, svarbesniu tampa raudonasis poslinkis. Dėl to tamsus nakties dangus patvirtina Hablo Visatos plėtimosi idėją.

Hablo konstantos nustatymas

Hablo konstanta apskaičiuojama išmatavus raudonąjį tolimųjų galaktikų poslinkį ir nustačius jų nuotolius. Hablo konstanta gali varijuoti, nes nustatinėjant galaktikų nuotolius remiamasi skirtingomis fizikinėmis prielaidomis. XX a. antrojoje pusėje buvo manoma, kad H₀ reikšmė yra tarp 50 ir 90 (km/s) /Mpc. Hablo konstanta tapo pagrindine ilgų ir aršių ginčų tarp Gérard de Vaucouleurs ir Allan Sandage priežastimi. Pirmasis jų teigė, kad H₀ reikšmė apytiksliai lygi 100, antrasis – 50. 1966 metais dėl šių dviejų Hablo konstantos reikšmių taip pat nesutarė Gustav Tammann ir Sidney van den Bergh, kuriems tarpininkavo John Bahcall. Nesutarimus iš dalies išsprendė Λ-CDM Visatos modelis (Λ - kosmologinė konstanta, CDM - šalta nematomoji medžiaga), sukurtas 10-ojo dešimtmečio pabaigoje. Naudojant šį modelį buvo pastebėtas aukštas raudonojo poslinkio lygis rentgeno spindulių ir mikrobangų ilgiuose. Stebėjimai buvo atlikti remiantis Sunyaev-Zel'dovich efektu, reliktinio spinduliavimo anizotropijų matavimais ir optiniais stebėjimais. Visais atvejais gauti rezultatai parodė, kad konstanta yra artima 70 (km/s) /Mpc.

Hablo parametro išvedimas

Pradedame nuo Frydmano lygties:

$H^{2}\equiv \left({\frac {\dot {a}}{a}}\right)^{2}={\frac {8\pi G\rho }{3}}-{\frac {kc^{2}}{a^{2}}}+\Lambda$

kur $H$ yra Hablo parametras, $a$ mastelio faktorius, G gravitacijos konstanta, $k$ Visatos geometrija („plokštumas“) lygi -1, 0 arba +1, ir $\Lambda$ kosmologinė konstanta.

Nuo medžiagos priklausanti Visata (su kosmologine konstanta)

Jeigu Visata yra medžiagiška, tai galima įvesti Visatos energijos tankį ρ kaip masę. Todėl:

$\rho =\rho _{m}(a)=\rho _{m0}a^{-3}{\frac {1}{1}}$

Čia ρ_m dabartinis medžiagos tankis. Žinoma, kad nereliatyvistinių dalelių energijos tankis mažėja proporcingai Visatos tūriui, todėl lygtis viršuje yra teisinga. Taip pat galime išreikšti (Ω_m žiūrėti tankio parametrą):

$\rho _{c}={\frac {3H^{2}}{8\pi G}}$

$\Omega _{m}\equiv {\frac {\rho _{m0}}{\rho _{c}}}={\frac {8\pi G}{3H_{0}^{2}}}\rho _{m0}$

taigi $\rho =\rho _{c}\Omega _{m}a^{-3}$. Pagal apibrėžimą

$\Omega _{k}\equiv {\frac {kc^{2}}{(a_{0}H_{0})^{2}}}$

ir

$\Omega _{\Lambda }\equiv {\frac {\Lambda H_{0}^{-2}}{3}}$

Čia nulinis apatinis indeksas reiškia dabartines reikšmes, o a₀ = 1. Visa tai įstačius į Frydmano lygtį ir pakeitus a kintamuoju a = 1/(1 + z) išeina:

$H^{2}(z)=H_{0}^{2}\left(\Omega _{M}(1+z)^{3}+\Omega _{k}(1+z)^{2}+\Omega _{\Lambda }\right)$

Nuo medžiagos ir tamsiosios energijos priklausanti Visata

Jei Visata priklauso nuo medžiagos ir tamsiosios energijos, tai viršutinė lygtis Hablo parametrui apskaičiuoti bus ir tamsiosios energijos būsenos funkcija, todėl:

$\rho =\rho _{m}(a)+\rho _{de}(a){\frac {1}{1}}$

Čia ρ_de yra tamsiosios energijos tankis. Kosmologijoje būsenos lygtis yra P = wρ, kurią įstatę į skysčio lygtį, rodančią, kaip su laiku kinta Visatos tankis, gauname:

${\dot {\rho }}+3{\frac {\dot {a}}{a}}\left(\rho +P\right)=0$

${\frac {d\rho }{dt}}=-3{\frac {da}{dt}}{\frac {1}{a}}\left(\rho +w\rho \right)$

${\frac {d\rho }{\rho }}=-3{\frac {da}{a}}\left(1+w\right)$

Jei w yra konstanta, tai

$\ln {\rho }=-3\left(1+w\right)\ln {a}$

$\rho =a^{-3\left(1+w\right)}e^{constant}$

Todėl tamsiajai energijai su pastovia būsenos w lygtimi – $\rho _{de}(a)=\rho _{de0}a^{-3\left(1+w\right)}$. Kaip ir anksčiau, įstatę tai į Frydmano lygtį ir laikydami, kad Visata yra plokščia, t. y. k = 0, gauname:

$H^{2}(z)=H_{0}^{2}\left(\Omega _{M}(1+z)^{3}+\Omega _{de}(1+z)^{-3\left(1+w\right)}\right)$

Jei tamsioji energija negali būti išreikšta pastovia lygtimi būsenai w, tada:

$\rho _{de}(a)=\rho _{de0}e^{-3\int {\frac {da}{a}}\left(1+w(a)\right)}$.

Sprendžiant šią lygtį, reikia parameterizuoti w(a), pavyzdžiui, w(a) = w0 + wa(1 − a). Tokiu atveju:

$H^{2}(z)=H_{0}^{2}\left(\Omega _{M}a^{-3}+\Omega _{de}a^{-3\left(1+w_{0}+w_{a}\right)}e^{-3w_{a}(1-a)}\right)$

Iš Hablo konstantos išvesti dydžiai

Hablo laikas

Hablo konstantos H₀ matavimo vienetai yra atvirkštinio laiko vienetai. Todėl Hablo laiką galime apibrėžti kaip 1/H₀. Standartiniame kosmologiniame modelyje Hablo laikas yra 4,35×10¹⁷ s, arba 13,8 milijardų metų, - kiek daugiau, nei siekia Visatos amžius.

Hablo nuotolis

Hablo nuotolis kosmologijoje reiškiamas c/H₀ – šviesos greitis padaugintas iš Hablo laiko – ir yra lygus 4228 milijonų parsekų, arba 13,8 milijardų šviesmečių. Pagal apibrėžimą skaitinė Hablo nuotolio išraiška šviesmečiais yra lygi skaitinei Hablo laiko išraiškai metais.

Hablo tūris

Hablo tūris kartais apibrėžiamas kaip c/H₀ dydžio Visatos tūris. Tikslaus apibrėžimo nėra: Hablo tūriu vadinamas arba c/H₀ spindulio sferos, arba c/H₀ kraštinės kubo tūris. Kai kurie kosmologai Hablo tūrį taiko stebimos Visatos tūriui apibūdinti, nors jos spindulys iš tiesų yra 3 kartus didesnis.

Atstumo skaičiavimas

Pagal Hablo dėsnį galima apskaičiuoti atstumą iki tolimųjų galaktikų. Pavyzdžiui, 1988 m. atrasta už 11,95 milijardo šviesmečių esanti galaktika, kuri tolsta v = 274 851 km/s greičiu (tai sudaro 91,7 % šviesos greičio).

Plėtimasis būtų stebimas iš bet kurio kito Visatos taško.

Straipsniai

• Kutner, Marc (2003). Astronomy: A Physical Perspective. Cambridge University Press. ISBN 0-521-52927-1.
• Hubble, E.P.., The Observational Approach to Cosmology (Oxford, 1937)
• Final Results from the Hubble Space Telescope Key Project to Measure the Hubble Constant. Freedman et al. The Astrophysical Journal, Volume 553, Issue 1, pp. 47-72.

Nuorodos

• Hablo konstantos istorija
• Hablo konstantos matavimas
• Hablo projektas
• Hablo diagrama