Puasono skirstinys
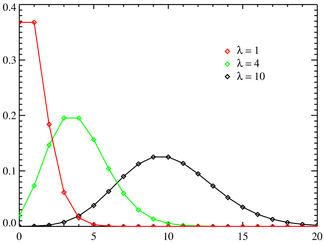
x ašyje atidėtas k. Funkcija turi prasmę tik su sveikais k. Ištisinės linijos nubrėžtos tik dėl vaizdumo ir tikrai nereiškia tolydumo pasiskirstymo dėsnyje
Puasono skirstinys – diskretus skirstinys (tikimybių pasiskirstymo dėsnis), nusakantis įvykių tikimybes įvykti per tam tikrą laiko intervalą, jeigu įvykiai vyksta pastoviu dažniu ir yra nepriklausomi vienas nuo kito. Šį dėsnį pirmasis aprašė prancūzų mokslininkas S. Puasonas.
Jei per tam tikrą laiko intervalą įvyksta vidutiniškai λ įvykių, tuomet tikimybė, kad per tą laiką įvyks tiksliai k įvykių bus lygi:[1]
Čia
- e yra natūrinių logaritmų pagrindas (e = 2.71828…),
- k yra įvykių skaičius (neneigiamas sveikas skaičius, k = 0, 1, 2, …), kurių tikimybę norime paskaičiuoti,
- k! yra k faktorialas,
- λ yra teigiamas realusis skaičius, vidutinis įvykių skaičius per tam tikrą laikotarpį. Tarkime, kad įvykiai vyksta vidutiniškai kas 4 minutės, o mes norime apskaičiuoti skaičių įvykių, įvyksiančių per 10 minučių. Tuomet turėsime naudoti Puasono skirstinį su λ = 10/4 = 2.5.
Puasono skirstinys gali būti išvestas iš binominio skirstinio kaip ribinis atvejis, tarus, kad p = λ/n ir įvykių skaičiui n artėjant į begalybę.
Pagrindiniai Puasono skirstinio momentai[redaguoti | redaguoti vikitekstą]
Taikymo pavyzdžiai[redaguoti | redaguoti vikitekstą]
Skirstinys taikomas aprašant korektūros klaidų puslapyje skaičių, avarijų keliuose per fiksuotą laiko tarpą skaičius, razinų bandelėje skaičių, telefono skambučių per valandą skaičių, gamybinių traumų per mėnesį skaičių, draudimo firmos išmokų per mėnesį skaičių, fotonų išlekiančių iš žvaigždės per laiko vienetą skaičių, lietaus lašų skaičių, radioaktyviajame skilime skilusių atomo branduolių skaičių ir pan.
Šaltiniai[redaguoti | redaguoti vikitekstą]
- ↑ Yates, Roy D.; Goodman, David J. (2005). Probability and Stochastic Processes. Hoboken, NJ: Wiley. ISBN 978-0-471-45259-1.



