Karno ciklas
| |
Šiam straipsniui ar jo daliai trūksta išnašų į patikimus šaltinius. Jūs galite padėti Vikipedijai pridėdami tinkamas išnašas su šaltiniais. |
Kiekviena termodinamikos sistema egzistuoja tam tikroje būsenoje (padėtyje). Kai sistema pereina per skirtingas arba tas pačias serijų padėtis ir galiausiai sugrįžta į savo pradinę padėtį, sakoma, jog įvyko termodinaminis ciklas. Vykstant šio ciklo procesui, sistema gali atlikti darbą jos aplinkoje, tuo būdu veikianti kaip šiluminis variklis. Karno ciklas yra ypatingas termodinaminis ciklas, pasiūlytas 1824 m. Nikolo Leonardo Sadi Karno ir išplėstas Benoito Pauliaus Emile Klapeirono 1830 ir 1840 m. Sistema, praeinanti Karno ciklą, tokiu atveju yra (spėjamas) Karno šiluminis variklis.
Šiluminis variklis veikia perduodant energiją iš šiltos srities į vėsų erdvės sritį ir proceso metu paverčiant dalį tos energijos į mechaninį darbą. Šis ciklas taip pat gali būti pakeistas priešingai. Sistema gali būti veikiama išorinės jėgos, o proceso metu ji gali perduoti šilumos energiją iš vėsesnės sistemos į šiltesnę sistemą, tuo būdu veikianti kaip šiluminis siurblys geriau nei šiluminis variklis.
Karno ciklas yra veiksmingiausias ciklas, galintis paversti duodamą šilumos energijos kiekį į darbą arba priešingai, duodamo darbo kiekio naudojimui šaldymo tikslais.
Karno ciklas[redaguoti | redaguoti vikitekstą]
Karno ciklas veikiantis kaip šiluminis variklis susideda iš šių etapų:
- Grįžtamasis izotermininis dujų plėtimasis esant "karštai" temperatūrai, TH (izoterminis šilumos papildymas). Per šį etapą (A į B paveikslėlyje 1, 1 į 2 pav. 2) besiplečiančios dujos atlieka stūmoklio darbą aplinkoje. Dujų plėtimasis varomas absorbcijos kiekiu Q1 karščio iš aukštos temperatūros šaltinio.
- Izentropinis (Grįžtamojo adiabatinio proceso, t. y. įvykstančio be šilumo praradimo ar įgijimo) dujų plėtimasis (izentropinis darbo našumas / išeiga). Dėl šio etapo (B į C paveikslėlyje 1, 2 į 3 pav. 2) stūmoklis ir cilindras turi prielaidą būti termiškai izoliuoti, tokiu būdu jie nei vienas, nei kitas neįgyja ar nepraranda šilumos. Dujos plečiasi toliau, atliekančios darbą apie aplinką. Dujų plėtimasis priverčia jas atvėsti iki "žemos" temperatūros, TC.
- Grįžtamasis izoterminis dujų suslėgimas esant "žemai" temperatūrai, TC. (izotermins karščio atmetimas) (C į D paveikslėlyje 1, 3 į 4 pav. 2) Dabar atliekamas darbas dujų aplinkoje, sukeliantis šilumos kiekį Q2 dujoms ištekėti į žemos temperatūros rezervuarą.
- Izentropinis dujų slėgimas (izentropoinis darbo našumas / išeiga). (D į A paveikslėlyje 1, 4 į 1 pav.) Dar kartą stūmoklis ir cilindras yra tariami termiškai izoliuoti. Šio etapo metu aplinka atlieka darbą dujoms, suslegianti jas ir priverčianti temperatūrą pakilti į TH. Šiuo metu dujos yra toje pačioje būsenoje kaip 1 etapo pradžioje.

Savybės ir reikšmės[redaguoti | redaguoti vikitekstą]
Temperatūros-entropijos diagrama[redaguoti | redaguoti vikitekstą]

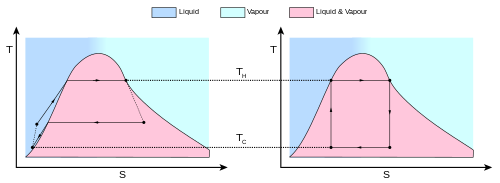
Karno variklio ar šaldytuvo funkcionavimas geriausiai yra suprantamas naudojant temperatūros-entropijos (TS) diagramą, kurioje termodinaminė būsena yra tiksliai nubrėžta iki taško kreivėje su entropija (S) kaip horizontali ašis ir temperatūra (T) kaip vertikali ašis. Sistemoje su fiksuotų dalelių skaičiumi, bet koks taškas grafike nusakys tam tikrą sistemos būseną. Termodinaminį procesą vaizduos kreivė, jungianti pradinę padėtį (A) ir galutinę padėtį (B). Plotas po kreive bus lygus:
kuris yra šiluminės energijos kiekis, perduotas (perneštas) proceso metu. Jeigu sistemos entropija didėja, plotas po kreive bus sistemos sugertos šilumos kiekis eigoje. Jeigu sistemos entropija mažėja, ji bus atiduotas šilumos kiekis. Vykstant bet kokiam cikliniam procesui bus aukštesnė ciklo dalis ir žemesnė dalis. Dėl ciklo, judančio pagal laikrodžio rodyklę, sritis žemiau aukštesnės dalies bus šilumos energija, sugerta (absorbuota) per ciklą, tuo tarpu sritis po žemesne dalimi bus šilumos energija, pašalinta per ciklą. Sritis ciklo viduje tada bus skirtumas tarp šių dviejų energijų. Bet kadangi sistemos vidinė energija turi būti grąžinta į savo pradinį dydį, šis skirtumas turi būti lygus darbui, kurį sistema atlieka per šį ciklą. Remiantis iliustracija 2, matematiškai grįžtamajam procesui galime rašyti, jog darbas, ciklinio proceso metu lygus:
Kadangi dU yra pilnas diferencialas, jo integralas bet kokiu uždaru kontūru yra lygus nuliui. Iš to išplaukia, kad plotas uždaro kontūro viduje T-S diagramoje yra lygus sistemos atliktam darbui.

Karno ciklas[redaguoti | redaguoti vikitekstą]
Aukščiau esančio integralo analizė yra ypač paprasta Karno ciklui. Energijos kiekis, kuris yra pernešamas (perduodamas) kaip darbas yra
Bendra šiluminės energijos, perduotos tarp karšto rezervuaro ir sistemos, suma bus
ir bendra šiluminės energijos, perduotos tarp sistemos ir šalto rezervuaro, suma bus
- .
Naudingumo koeficientas yra apibūdinamas kaip:
kur
- yra darbas, atliktas sistemos (energija, išeinanti iš sistemos kaip darbas),
- šiluma, sukelta sistemoje (šilumos energija, įeinanti į sistemą),
- yra šalto rezervuaro absoliutinė temperatūra, o
- yra karšto rezervuaro absoliutinė temperatūra.
- yra maksimali (didžiausia) sistemos entropija
- yra minimali (mažiausia) sistemos entropija
Naudingumo koeficientas turi prasmę šiluminiam varikliui, nes yra šilumos energijos dalelė, išgauta iš karšto rezervuaro ir paversta į mechaninį darbą.
Karno teorema[redaguoti | redaguoti vikitekstą]
Tai galima matyti aukščiau esančioje diagramoje, kuri bet kokiam darbo ciklui tarp temperatūrų ir nė kiek negali viršyti Karno ciklo naudingumo koeficiento.
Karno teorema yra formalus šio fakto trumpas išdėstymas: Nė vienas variklis, veikiantis tarp dviejų šilumos rezervuarų negali būti efektyvesnis nei Karno variklis, veikiantis tarp tų pačių rezervuarų. Taigi, Lygtis 3 duoda maksimalų naudingumo koeficientą, galimą bet kokiam varikliui, naudojančiam atitinkamas temperatūras. Išvada Karno teoremai teigia, jog: Visi grįžtami varikliai, veikiantys tarp tų pačių šilumos rezervuarų yra vienodai veiksmingi. Pertvarkant lygties dešiniąją pusę duoda tai, kas gali būti lengviau suprantama lygties forma. Būtent, kad teorinis didžiausias šiluminio variklio naudingumo koeficientas yra lygus temperatūros skirtumui tarp karšto ir šalto rezervuaro padalinus iš karšto rezervuaro absoliutinės temperatūros. Norint rasti absoliutinę temperatūrą kelvinais, reikia pridėti 273.15 laipsnius prie Celsijaus temperatūros. Žvelgiant į šią formulę galime pastebėti įdomų efektą. Sumažinant šalto rezervuaro temperatūrą, didesnį poveikį turės šiluminio variklio ribos efektyvumui negu padidinant karšto rezervuaro temperatūrą ta pačia suma. Realiame pasaulyje tai gali būti sunku pasiekti, nes šaltas rezervuaras dažnai yra egzistuojanti aplinkos temperatūra.
Kitais žodžiais, didžiausias veiksmingumas (t. y. naudingumo koeficientas) yra pasiekiamas tik tada, kai cikle nėra sukurtos naujos entropijos. Priešingu atveju, kadangi entropija yra būsenos funkcija, reikalingas šilumos išmetimas į aplinką, norint atsikratyti perteklinės entropijos, lemiantis efektyvumo sumažėjimą. Todėl 3 lygtis parodo bet kokio grįžtamojo šiluminio variklio naudingumo koeficientą.
Realių šiluminių variklių efektyvumas[redaguoti | redaguoti vikitekstą]
Karno suprato, jog realybėje nėra įmanoma sukurti termodinaminį grįžtamąjį variklį, taigi realūs šiluminiai varikliai yra mažiau veiksmingesni negu kaip nurodyta 3 – ioje Lygtyje. Vis dėlto, Lygtis 3 yra labai naudinga nustatant maksimalų naudingumo koeficientą, kuris kada nors galėtų būti tikėtinas šilumos rezervuarų.
Nors Karno ciklas yra idealizavimas, Karno naudingumo koeficiento išraiška yra labai svarbi. Turint omenyje vidutines temperatūras,
kuriomis šiluma yra tiekiamas galingumas ir našumas (t. y. gamybinis pajėgumas, galia) nurodyta tvarka. Atitinkamai pakeičiant TH ir TC Lygtyje (3) <TH> ir <TC>.
Karno ciklui ar jo atitikmeniui, <TH> yra aukščiausia pasiekiama temperatūra ir <TC> žemiausia. Kitiems mažiau efektyviems ciklams, <TH> bus žemesnė negu TH , o <TC> bus aukštesnė negu TC. Tai gali padėti paaiškinti, pavyzdžiui, kodėl pakartotinas pašildytojas arba regeneratorius gali pagerinti šilumos efektyvumą.
Taip pat skaitykite[redaguoti | redaguoti vikitekstą]
- Rankine ciklas
- Karno šiluminis variklis
- Grįžtamas procesas (termodinamika)
- Karno ciklo grafikai (viršuje) neturėtų būti maišomi su Karnaugho žemėlapiais Būlio logika ir skaitmenine elektronika















