Dvigubo plyšio eksperimentas
Dvigubo plyšio eksperimentas, dar vadinamas Jungo eksperimentu – demonstracija, parodanti, kad medžiaga ir energija turi bangos ir dalelės savybių, kas parodo iš esmės tikimybinį kvantinės mechanikos reiškinį. Paprastoje eksperimento versijoje koherentinis šviesos šaltinis, toks kaip lazeris, šviečiamas ant plonos plokštelės, perdurtos dviem plyšiais. Šviesa, praėjusi pro šiuos plyšius, matoma už plokštelės esančiame ekrane. Banginis šviesos pobūdis verčia pro plyšį praėjusias šviesos bangas interferuoti, ekrane sukuriant šviesias ir tamsias juostas – tai būtų neįmanoma, jeigu šviesą sudarytų tik dalelės. Tačiau ekrane šviesa visuomet atrodo susigėrusi lyg būtų sudaryta iš pavienių dalelių ar fotonų.[1] Tai sukuria principą, kuris dar žinomas kaip bangos ir dalelės dvilypumas. Be to, pavienių fotonų detekcija iš prigimties laikoma tikimybine, kas yra nepaaiškinama naudojantis vien klasikine mechanika.[2]
Apžvalga[redaguoti | redaguoti vikitekstą]

Jeigu šviesa būtų griežtai sudaryta iš klasikinių dalelių ir tos dalelės būtų paleistos tiesiai pro plyšį, leidžiant atsimušti į kitoje pusėje esantį ekraną, mes išvystume plyšio dydį ir formą atitinkantį atspindį. Tačiau kai šis „vieno plyšio eksperimentas“ yra atliekamas, vaizdas ekrane yra difrakcinis atspindys, pakankamai siaura centrinė šviesos juosta su lygiagrečiomis silpnesnio ryškio juostomis abiejuose pusėse (žr. 1 paveikslėlį dešinėje).
Lygiai taip pat, jeigu šviesa būtų griežtai sudaryta iš klasikinių dalelių ir mes apšviestume du lygiagrečius plyšius, tai ekrane matomas atspindys būtų sudarytas iš dviejų atskirų plyšių. Tačiau realybėje šis atspindys yra daug platesnis ir detalesnis, apimantis tamsių ir šviesių juostų seriją (2 pav. dešinėje). Kai Tomas Jungas pirmasis atliko šį eksperimentą, tai parodė, kad šviesą sudaro bangos – ryškumo pasiskirstymas galėjo būti paaiškinamas pakaitomis sudedant arba atimant bangos fronto trukdžius (interferenciją).[2] Jungo eksperimentas suvaidino svarbų vaidmenį šviesos bangų teorijos pripažinime XIX a. pradžioje, į šoną nustumiant Izaoko Niutono pasiūlytą korpuskulinę šviesos teoriją, vyravusią XVII–XVIII a. Tačiau vėlesnis fotoefekto atradimas pademonstravo, kad esant kitokioms sąlygoms šviesa gali funkcionuoti tarsi būtų sudaryta iš diskrečių dalelių. Šie tariamai prieštaringi atradimai paskatino peržengti klasikinės mechanikos ribas ir atsižvelgti į šviesos pobūdį kvantinėje mechanikoje.
Dvigubo plyšio eksperimentas (ir jo variacijos), atliekamas su individualiomis dalelėmis, dėl savo aiškumo nagrinėjant kvantinės mechanikos galvosūkius tapo klasikiniu minties eksperimentu. Kadangi išaiškėdavo stebėtojui taikomi esminiai apribojimai bandant nustatyti eksperimento rezultatus, Ričardas Feinmanas tai pavadino „reiškiniu, kurio neįmanoma… paaiškinti bet kokiu paprastu būdu ir kuriame slypi kvantinės mechanikos esmė. Realybėje, jame slypi vienintelė [kvantinės mechanikos] mįslė.“[2], ir laikėsi optimistinės nuomonės, jog visos kvantinės mechanikos žinios gali būti surinktos permąstant šio eksperimento išvadas.[3]
Klasikinė bangų optikos formuluotė[redaguoti | redaguoti vikitekstą]
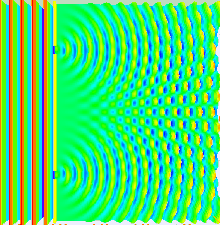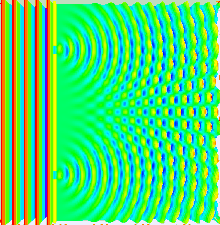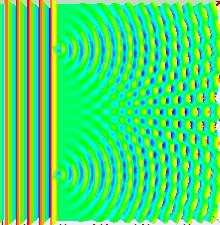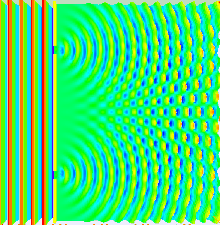


Didžioji šviesos būvio dalis gali būti pademonstruota naudojantis klasikine bangų teorija. Vienas iš būdų yra Hiugenso ir Frenelio principas, nusakantis, jog kiekvienas bangos taškas bangos fronte sukuria antrinę sferinę bangelę ir kad bet koks trikdys paskesniame taške gali būti randamas susumuojant pavienių bangelių įtaką tame taške. Sumuojant reiktų atsižvelgti į pavienių bangelių fazę ir amplitudę. Reikia pabrėžti, jog išmatuoti galima tik tai šviesos lauko intensyvumą, kuris proporcingas amplitudės kvadratui.
Dvigubo plyšio eksperimente du plyšiai apšviečiami vienu lazerio spindulių pluoštu. Jeigu plyšių plotis yra pakankamai mažas (mažesnis negu lazerio bangos ilgis), tai plyšiai šviesą išsklaido į cilindrines bangas. Šie du cilindriniai bangų frontai yra persikloję ir amplitudė (taip pat ir intensyvumas) bet kuriame taške susijungus bangų frontams priklauso nuo ryškio ir dviejų bangos frontų fazių. Fazių skirtumas tarp bangų nustatomas dviejų bangų nukeliautų atstumų skirtumu.
Jeigu stebimasis atstumas yra žymus lyginant su plyšius skiriančiu atstumu (tolimasis laukas), fazių skirtumas gali būti randamas naudojantis geometrija, parodyta dešinėje (4 pav.). Kelio skirtumas tarp dviejų bangų keliaujant kampu θ yra:
Kai dvi bangos yra fazėje, t. y. nukeliauto kelio skirtumas lygus sveikajam bangos ilgio skaičiui, tada susumuota amplitudė ir taip pat susumuotas intensyvumas yra maksimalūs, o kai jos yra antifazėje, t. y. nukeliauto kelio skirtumas lygus pusei, pusantro bangos ilgio ir t. t., tada dvi bangos nutrūksta ir susumuotas intensyvumas yra nulinis. Šis efektas žinomas kaip interferencija. Interferencijos pakraščių maksimumas pasitaiko tokiuose kampuose
kur λ yra šviesos bangos ilgis. Kampinis tarpas tarp pakraščių yra ir randamas
Tarpas tarp plyšių pakraščių atstume randamas
Pavyzdžiui, jeigu du plyšiai yra atskirti 0,5 mm (d) ir jie yra apšviečiami matomos šviesos diapazonu: 0,6 μm bangos ilgio lazeriu (λ), tada 1 m atstume (z), tarpas tarp pakraščių bus lygus 1,2 mm.
Jeigu plyšių plotis b yra didesnis už bangos ilgį, tada Fraunhoferio difrakcijos lygtis pateikia tokį išsklaidytos šviesos intensyvumą:[4]
Taip pat skaitykite[redaguoti | redaguoti vikitekstą]
Išnašos[redaguoti | redaguoti vikitekstą]
- ↑ Darling, David (2007). „Wave - Particle Duality“. The Internet Encyclopedia of Science. The Worlds of David Darling. Nuoroda tikrinta 2008-10-18.
- ↑ 2,0 2,1 2,2 Feynman, Richard P.; Robert Leighton, Matthew Sands (1965). The Feynman Lectures on Physics, Volume III. Massachusetts, USA: Addison-Wesley. pp. 1–1 to 1–9. ISBN 0-201-02118-8P.
{{cite book}}: Patikrinkite|isbn=reikšmę: invalid character (pagalba) - ↑ Greene, Brian (1999). The Elegant Universe: Superstrings, Hidden Dimensions, and the Quest for the Ultimate Theory. New York: W.W. Norton. pp. 97–109. ISBN 0-393-04688-5.
- ↑ Jenkins FA and White HE, Fundamentals of Optics, 1967, McGraw Hill, New York
Literatūra[redaguoti | redaguoti vikitekstą]
- Al-Khalili, Jim (2003). Quantum: A Guide for the Perplexed. London: Weidenfeld and Nicholson. ISBN 0-297-84305-2.
- Feynman, Richard P. (1988). QED: The Strange Theory of Light and Matter. Princeton University Press. ISBN 0-691-02417-0.
- Frank, Philipp (1957). Philosophy of Science. Prentice-Hall.
- French, A.P.; Taylor, Edwin F. (1978). An Introduction to Quantum Physics. Norton. ISBN 0-393-09106-6.
- Greene, Brian (2000). The Elegant Universe. Vintage. ISBN 0-375-70811-1.
- Greene, Brian (2005). The Fabric of the Cosmos. Vintage. ISBN 0-375-72720-5.
- Gribbin, John (1999). Q is for Quantum: Particle Physics from A to Z. Weidenfeld & Nicolson. ISBN 0-7538-0685-1.
- Hey, Tony (2003). The New Quantum Universe. Cambridge University Press. ISBN 0-521-56457-3.
- Sears, Francis Weston (1949). Optics. Addison Wesley.
- Tipler, Paul (2004). Physics for Scientists and Engineers: Electricity, Magnetism, Light, and Elementary Modern Physics (5th leid.). W. H. Freeman. ISBN 0-7167-0810-8.







![{\displaystyle {\begin{aligned}I(\theta )&\propto \cos ^{2}\left[{\frac {\pi d\sin \theta }{\lambda }}\right]~\mathrm {sinc} ^{2}\left[{\frac {\pi bsin\theta }{\lambda }}\right]\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/398474b04ac51479d1f19b5be1789ee526b36b92)