Burbulo rikiavimo algoritmas

| Algoritmas | |
| Tipas | Rikiavimo algoritmai |
| Pavadinimas | Burbulo (Bubble Sort) |
| Sudėtingumas | Vidutinis - N²; blogiausias - N² |
| Greitos nuorodos | |
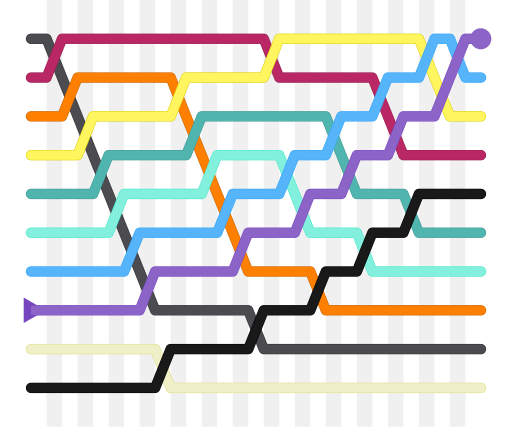
Burbulo rikiavimo metodas – vienas iš paprastų, bet nelabai efektyvių rikiavimo algoritmų. Algoritmo principas – nuosekliai iš eilės peržiūrėti gretimų elementų poras, prireikus elementus sukeisti, perkeliant mažesnį arčiau pradžios. Tokiu būdu per pirmą iteraciją mažiausias elementas perkeliamas į pirmą poziciją, vėliau tas pats principas taikomas posekiui be pirmo elemento ir t. t.
Algoritmo veikimo principas primena virimo procesą, kai oro burbulai kyla į paviršių, dėl to jis ir yra taip vadinamas.[1]
Burbulo algoritmas N elementų masyvo rikiavimui naudoja apie N²/2 lyginimų ir N²/2 keitimų vietomis, tiek laukiamu, tiek ir blogiausiu atveju. Algoritmas nenaudoja papildomos atminties.
Algoritmo vykdymas pažingsniui
[redaguoti | redaguoti vikitekstą]Naudosime skaičių masyvą „5 1 4 2 8“ ir jį surūšiuosime nuo mažiausio elemento iki didžiausio. Kiekviename žingsnyje paryškinti elementai yra palyginami.
Pirmas praėjimas:
(5 1 4 2 8) (1 5 4 2 8) Čia algoritmas palygina pirmus 2 elementus ir juos apkeičia vietomis.
(1 5 4 2 8) (1 4 5 2 8)
(1 4 5 2 8) (1 4 2 5 8)
(1 4 2 5 8) (1 4 2 5 8) Dabar elementai yra išdėstyti tinkama tvarka, todėl algoritmas jų neapkeičia vietomis.
Antras praėjimas:
(1 4 2 5 8) (1 4 2 5 8)
(1 4 2 5 8) (1 2 4 5 8)
(1 2 4 5 8) (1 2 4 5 8)
(1 2 4 5 8) (1 2 4 5 8)
Dabar masyvo elementai išdėstyti tinkama tvarka, bet algoritmas to nežino. Algoritmui reikia vieno praėjimo be pakeitimų, kad žinotų jog elementai reikiama tvarka.
Trečias praėjimas:
(1 2 4 5 8) (1 2 4 5 8)
(1 2 4 5 8) (1 2 4 5 8)
(1 2 4 5 8) (1 2 4 5 8)
(1 2 4 5 8) (1 2 4 5 8)
Galiausiai algoritmas baigė savo darbą.
Pavyzdžiai
[redaguoti | redaguoti vikitekstą]- Realizacija Pascal kalba:
procedure Burbulas(var a:array of integer; N:integer);
var i, j, t: integer;
begin
for i:=N downto 1 do
for j:=2 to i do
if a[j-1]>a[j] then
begin
t:=a[j-1];
a[j-1]:=a[j];
a[j]:=t;
end
end;
- Realizacija C++ kalba:
#include <iostream>
using namespace std;
int main()
{
int N;
cout << "Kiek bus skaiciu?" << endl;
cin >> N;
int a[N];
cout << "Kokie bus skaiciai?" << endl;
for (int i=1; i<=N; i++)
cin >> a[i];
for (int i=1; i<=N; i++)
for (int j=2; j<=N; j++)
if (a[j-1]>a[j])
{
int t=a[j-1];
a[j-1]=a[j];
a[j]=t;
}
cout << "Surikiuoti skaiciai" << endl;
for (int i=1; i<=N; i++)
cout << a[i] << endl;
}
- Realizacija Java kalba:
public class Pavyzdys {
...
private int[] duomenys;
private final int ilgis;
...
private void rikiuotiBurbuliuku() {
boolean testi = true;
int pask = ilgis – 1;
while (testi) {
testi = false;
for (int i=0;i<pask;++i) {
if (duomenys[i] > duomenys[i+1]) {
int laikinas = duomenys[i];
duomenys [i] = duomenys [i+1];
duomenys[i+1] = laikinas;
testi = true;
}
}
--pask;
}
}
...
}
- Realizacija PHP kalba:
function bubble_sort($array){
$count = count($array);
if ($count <= 0) return false;
for($i=0; $i<$count; $i++){
for($j=$count-1; $j>$i; $j-–){
if ($array[$j] < $array[$j-1]){
$tmp = $array[$j];
$array[$j] = $array[$j-1];
$array[$j-1] = $tmp;
}
}
}
return $array;
}
Šaltiniai
[redaguoti | redaguoti vikitekstą]- ↑ Algimantas Juozapavičius. Duomenų struktūros ir efektyvūs algoritmai. – Vilnius: TEV, 2007. – 65 p. – ISBN 978-9955-680-87-1

