Vilnelė (matematika)
 Šis straipsnis apie matematinių funkcijų klasę. Apie upę skaitykite straipsnyje Vilnia.
Šis straipsnis apie matematinių funkcijų klasę. Apie upę skaitykite straipsnyje Vilnia.


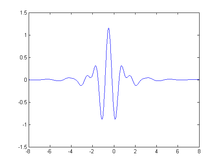

Vilnelė (angl. wavelet nuo pranc. ondelette - maža bangelė) - funkcija, leidžianti tirti signalų dažninius komponentus atskiruose laiko intervaluose (naudojant vilnelių transformacijas).
Pagal vieną iš apibrėžimų, vilnele vadinama funkcija, kurios vidurkis yra lygus nuliui:[1]
Įrodoma, kad funkcijos, kuriai teisingos sąlygos
ir
kitaip tariant,
vidurkis yra lygus nuliui, jei ji tenkina priimtinumo sąlygą:[1]
čia yra vilnelės Furjė transformacija.
Pagal kitą apibrėžimą, vilnele vadinama funkcija iš Hilberto erdvės, iš kurios galima suformuoti funkcijų šeimą, sudarančią ortonormuotą bazę Hilberto erdvėje, naudojant formulę:[1]
Vilnelė ar vilnelių šeima gali būti nusakyta įvairiais būdais, pavyzdžiui, motinine vilnele ir mastelio funkcija. Turint motininę vilnelę, gali būti rastos vilnelės kitiems masteliams ir laikams:
Istorija[redaguoti | redaguoti vikitekstą]
Pirmąja vilnele laikoma Haaro vilnelė, pasiūlyta 1909 m. vengrų matematiko Alfredo Haaro.[2] 1980 m. Jean Morlet ir Alexander Grossmann pateikė vilnelės apibrėžimą kvantinėje fizikoje.[2] 1985 m. Stéphane G. Mallat aptiko ryšių tarp kvadratūrinių veidrodinių filtrų, piramidinių algoritmų ir ortonormaliųjų vilnelių bazių.[2] Iš dalies naudodamasis šiais rezultatais Yves F. Meyer suformavo pirmąsias netrivialias vilneles.[2] 1987 m. Ingrid Daubechies suformavo vieną iš pagrindinių vilnelių bazių.[2]
Išnašos[redaguoti | redaguoti vikitekstą]
- ↑ 1,0 1,1 1,2 Abul Hasan Siddiqi "Applied functional analysis. Numerical Methods, Wavelet Methods and Image Processing", Marcell Dekker, Inc., 2004
- ↑ 2,0 2,1 2,2 2,3 2,4 A. Graps, "An introduction to wavelets", "IEEE Computational Science & Engineering", Vol. 2, Issue 2, Summer 1995, p. 50-61, ISSN: 1070-9924, [1] Archyvuota kopija 2007-06-14 iš Wayback Machine projekto.
Nuorodos[redaguoti | redaguoti vikitekstą]
- The Wavelet Digest Archyvuota kopija 2020-09-29 iš Wayback Machine projekto.








