Radialinis greitis
| |
Šiam straipsniui ar jo daliai trūksta išnašų į patikimus šaltinius. Jūs galite padėti Vikipedijai pridėdami tinkamas išnašas su šaltiniais. |
Radialinis greitis – objekto greitis išilgai regėjimo spindulio OA arba, kitais žodžiais tariant, tai taško A greičio projekcija į tiesę (OA), jungiančią tą tašką ir koordinačių pradžią, O.
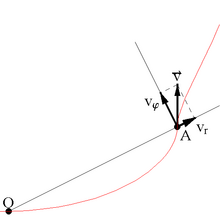
Pagal apibrėžimą, radialinis greitis yra skaliarinis dydis:
,
kur – vienetinis vektorius, nukreiptas radiuso vektoriaus kryptimi.
Pilnas greitis susidėtų iš radialinės ir tangentinės greičių komponenčių:
.
Radialinis greitis visada bus lygus išraiškai:
Pagal sutarimą, jei taškas A artėja, , jei tolsta, .
Astronomijoje dėl Doplerio reiškinio tolstančio objekto spinduliuojamos šviesos bangos ilgis pasislinks į raudonąją pusę, jei objektas artės – į mėlynąją pusę.
Tolimojo dangaus objekto radialinis greitis nustatomas iš aukštos skiriamosios gebos spektrų, lyginant pasirinktos matuojamos linijos bangos ilgį su tos pačios linijos bangos ilgiu, gautu laboratorinėmis sąlygomis (tai yra ).
Daugelyje dvinarių žvaigždžių judėjimas orbita sukelia radialinio greičio kitimus iki kelių kilometrų per sekundę. Kadangi tokių žvaigždžių spektrai kinta dėl Doplerio efekto, jos yra vadinamos spektroskopinėmis dvinarėmis žvaigždėmis.
Radialinio greičio kitimo analizė leidžia įvertinti dvinarių žvaigždžių mases ir kai kuriuos orbitų elementus, pavyzdžiui, ekscentricitetas ir didžioji pusašė. Tuo pat būdu galima aptikti ir planetas prie kitų žvaigždžių. Tačiau iš radialinių greičių analizės mes galime nustatyti tik apatinę planetos masės ribą, kadangi didelės masės planetos, kurių orbitos smarkiai pasvirusios regėjimo spindulio atžvilgiu radialinio greičio kitimo amplitudė bus mažesnė – taip pat, kaip ir mažesnės masės planetos, kurios orbitos plokštuma sutampa su regėjimo spinduliu.









