Paskalio trikampis

Matematikoje Paskalio trikampis arba aritmetinis trikampis – trikampė skaičių lentelė binominiams koeficientams gauti.[1] Geometrinis derinių išdėstymas. Paskalio trikampis yra pavadintas jį tyrinėjusio prancūzų fiziko ir matematiko Blezo Paskalio (1623–1662) vardu, bet jis buvo atrastas bei studijuotas ir daug anksčiau.
Konstrukcija[redaguoti | redaguoti vikitekstą]

Paskalio trikampio konstravimas prasideda nuo vieneto parašymo. Tai yra nulinė trikampio eilutė. Sekančiose eilutėse elementus galima rasti sudėjus du virš jo esančius skaičius. Jei kurio nors iš viršutinių skaičių nėra, jo vietoje reikia įstatyti nulį. Pavyzdžiui, pirmoje eilutėje pirmas skaičius gaunamas viršutinėje dešinėje pusėje esantį vienetą sudėjus su įsivaizduojamu nuliu viršutinėje kairėje pusėje. O sudėjus trečios eilutės skaičius 1 ir 3 gaunamas ketvirtos eilutės skaičius 4. Remiantis formule Paskalio trikampį galima tęsti be galo.
n – tosios trikampio eilutės k – tasis elementas yra lygus derinio reikšmei. Paskalio trikampis konstruojamas pagal derinių savybę . Pavyzdžiui, , todėl sudėjus antros eilutės nulinį ir pirmąjį narius gaunamas trečios eilutės pirmas numeris (reikia turėti omenyje, kad ir eilutės, ir eilučių elementai numeruojami pradedant nuliu, o ne vienetu).
Trikampis[redaguoti | redaguoti vikitekstą]
Žemiau yra pavaizduotas Paskalio trikampis iki šešioliktosios eilutės.
Panaudojimas[redaguoti | redaguoti vikitekstą]
Dvinarių skleidiniai[redaguoti | redaguoti vikitekstą]
Paskalio trikampis nusako išskleistų dvinarių koeficientus. Pvz.:
- (x + y)² = x² + 2xy + y² = 1x²y0 + 2x1y1 + 1x0y².
Reikia pastebėti, kad koeficientai 1, 2, 1 yra antrosios Paskalio trikampio eilutės numeriai. Bendra x + y tipo dvinarių pakeltų natūraliuoju skaičiumi iškleidimo formulė yra
- (x + y)n = a0xn + a1xn−1y + a2xn−2y² + … + an−1xyn−1 + anyn,
kur koeficientai ai yra n – tosios Paskalio trikampio eilutės skaičiai. Matematiškai tą būtų galima užrašyti taip:
arba
Tai yra Binomo formulė.
Panaudojimas kombinatorikoje[redaguoti | redaguoti vikitekstą]
Paskalio trikampis taip pat gali būti naudojamas derinių skaičiavimui. Jei reikia sužinoti, kiek skirtingų būdų yra pasirinkti k daiktų, jei iš viso yra n daiktų, tą galime suskaičiuoti pagal formulę:
Kadangi būtent ši formulė apskaičiuoja ir Paskalio trikampio n – tosios eilutės k – tąjį elementą, vietoje skaičiavimų kartais yra patogiau pasinaudoti trikampiu. Pavyzdžiui, turime 12 krepšininkų ir norime sužinoti, kiek skirtingų starto penketukų yra įmanoma iš jų sudaryti. Iš pradžių reiktų surasti dvyliktą Paskalio trikampio eilutę (turint omeny, kad pirmoji eilutė yra nulinė) ir tada rasti tos eilutės penktąjį elementą (vėlgi turint omeny, kad pirmasis parašytas skaičius yra nulinis eilutės elementas). Šiu atveju atsakymas būtų 792.
Savybės[redaguoti | redaguoti vikitekstą]
- Kiekviena piramidės eilutė yra simetriška
- Pirmąsias įstrižaines abejose piramidės pusėse sudaro vienetai, antrąsias – natūralieji skaičiai savo tvarka, trečiąsias – trikampiai skaičiai, ketvirtąsias – kvadratiniai skaičiai ir t. t.
- n – tosios eilutės skaičių suma yra lygi 2n. Pavyzdys: ketvirtosios eilutės skaičių suma yra 1 + 4 + 6 + 4 + 1 = 16 = 24.

- Bet kokio ilgio žemyn einančios ir vienetu prasidedančios įstrižainės narių suma lygi skaičiui, esančiam po paskutinio atkarpos elemento, bet nepratęsiančiam įstrižainės. Dešinėje esančiame piešinyje pateikti keli šios savybės pavyzdžiai:
- 1 + 1 + 1 + 1 + 1 = 5
- 1 + 3 + 6 = 10
- 1 + 3 + 6 + 10 + 15 = 35
- 1 + 6 + 21 = 28
Ši savybė kartais yra vadinama ledo ritulio lazdos struktūra.
- n – tosios eilutės skaičių kvadratų suma yra lygi 2*n – tosios eilutės viduriniam elementui. Pavyzdys: ketvirtosios eilutės kvadratų suma yra . Tai reiškia, kad aštuntosios eilutės vidurinis elementas taip pat yra 70. Apibendrinus, galima užrašyti formulę:
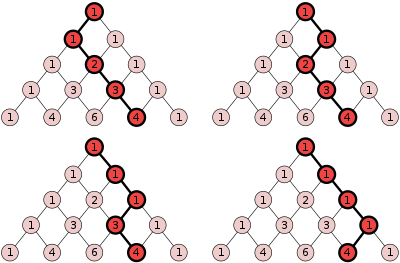
- Įsivaizduokite, kad trikampis yra takų, jungiančių trikampio numerius, rinkinys. Skirtingų būdų nueiti į kiekvieną numerį kiekis būtų lygus numeriui į kurį eitume (čia eiti atgal negalima). Žemiau pateiktas pavyzdys su skaičiumi su skaičiumi 4, į kurį nueiti yra 4 būdai.

- Jei į n – tosios eilutės numerius žiūrėtume kaip į vieno skaičiaus skaitmenis, tai tas skaičius būtų lygus 11n. Pavyzdys: trečiąją eilutę 1, 3, 3, 1 paverčiame skaičiumi 1331. Tada pastebime, kad 1331 = 11³. Penkta eilutė, kurią sudaro numeriai 1, 5, 10, 10, 5, 1, pasiverstų į skaičių 161051, nes dviženklių skaičių reikšmes reiktų perkelti į priekį arba, kitaip tariant, pirmuosius dviženklių numerių skaitmenis pridėti prie prieš tai einančio numerio.
- Nuspalvinus visus nelyginius Paskalio trikampio skaičius gaunama struktūra, kuri yra labai panaši į fraktalą, vadinamą Sierpinskio trikampiu. Kuo didesnį Paskalio trikampį paimsime, tuo panašumas bus didesnis. Riboje, kai eilučių skaičius artėja prie begalybės, gauta struktūra ne tik primintų, bet ir būtų Sierpinskio trikampis, jei tik perimetras būtų pastovus. Nuspalvinus visus skaičius, kurie nesidalina iš 3, 4 arba kokio nors kito skaičiaus, gaunamos kitokios struktūros.

|

|
| Nuspalvoti nelyginiai skaičiai | Nuspalvoti iš 3 nesidalijantys skaičiai |

|

|
| Nuspalvoti iš 4 nesidalijantys skaičiai | Nuspalvoti iš 5 nesidalijantys skaičiai |
Taip pat skaitykite[redaguoti | redaguoti vikitekstą]
Šaltiniai[redaguoti | redaguoti vikitekstą]
- ↑ aritmetinis trikampis. Visuotinė lietuvių enciklopedija (tikrinta 2024-02-03).









