Kvaternijonas

Paminklinė lenta žyminti vietą, kur Hamiltonas sugalvojo kvaternijonus

Kvaternijonas (lot. quattor – keturi) – skaičių aibė, nekomutatyvus kompleksinių skaičių aibės praplėtimas. Kvaternijono koncepciją sumanė airis Viljamas Rovanas Hamiltonas 1843 m.

Apibrėžimas

Kvaternijonų daugyba

·	1	i	j	k
1	1	i	j	k
i	i	−1	k	−j
j	j	−k	−1	i
k	k	j	−i	−1

Jei kompleksiniai skaičiai gaunami prie realiųjų skaičių pridedant įsivaizduojamą elementą $i$, kur $i^{2}=-1$, kvaternijonų aibė gaunama pridedant tris elementus $i$, $j$ ir $k$, tenkinančius tokias sąlygas:

$i^{2}=j^{2}=k^{2}=ijk=-1$

Kiekvienas kvaternijonas užrašomas formule:

$a+bi+cj+dk$

Savybės

Skirtingai, nei realių ar kompleksinių skaičių, kvaternijonų daugyba yra nekomutatyvi, t. y. $ij=k$, bet $ji=-k$.

Kvaternionų ciklinės sandaugos diagrama.

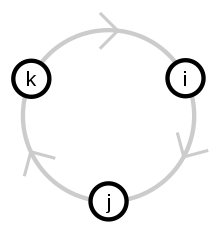
Taip pat menamųjų komponenčių porų sandaugų rezultatą galima vaizduoti cikline diagrama. Gretimų dviejų komponenčių sandauga nurodyta kryptimi yra lygi sekančiai komponentei, pvz.: $ij=k$, $jk=i$. Dauginant komponenčių poras priešinga kryptimi nei rodyklėmis nurodyta diagramoje gaunama trečia komponentė su neigiamu ženklu, pvz.: $kj=-i$. Tą patį rezultatą galite matyti ir kvaternijonų daugybos lentelėje.

Vaizdavimas matricomis

Kvaternijonus galima vaizduoti 2×2 dydžio kompleksinių skaičių matrica arba 4×4 dydžio realiųjų skaičių matrica. Taigi, kvaternijoną $a+bi+cj+dk$ galima užrašyti:

${\begin{pmatrix}a-di&-b+ci\\b+ci&\;\;a+di\end{pmatrix}}$

Arba:

${\begin{pmatrix}\;\;a&-b&\;\;d&-c\\\;\;b&\;\;a&-c&-d\\-d&\;\;c&\;\;a&-b\\\;\;c&\;\;d&\;\;b&\;\;a\end{pmatrix}}$

Panaudojimas

Kvaternijonai naudojami kompiuterinėje grafikoje objektų transformavimui trimatėje erdvėje. Kvaternijonai taip pat naudojami signalų apdorojime, fizikoje.