Ermito polinomas

Ermito polinomas matematikoje – polinomas, priklausantis ortogonalių polinomų sekai, kurį atsiranda tikimybių teorijos problemose, kombinatorikoje bei fizikoje.

Apibrėžimas

Ermito polinomai yra apibrėžiami arba sąryšiu

$H_{n}(x)=(-1)^{n}e^{x^{2}/2}{\frac {d^{n}}{dx^{n}}}e^{-x^{2}/2}\,\!$

("tikimybiniai Ermito polinomai"), arba kartais kitu sąryšiu

$H_{n}(x)=(-1)^{n}e^{x^{2}}{\frac {d^{n}}{dx^{n}}}e^{-x^{2}}\,\!$

("fizikiniai Ermito polinomai"). Šie du apibrėžimai nėra tiksliai vienodi, vienas yra kito mastelio keitimas

$H_{n}^{\mathrm {fiz} }(x)=2^{n/2}H_{n}^{\mathrm {tik} }({\sqrt {2}}\,x).\,\!$

Tradiciškai matematikoje naudojamas pirmas apibrėžimas, kadangi

${\frac {1}{\sqrt {2\pi }}}e^{-x^{2}/2}$

yra tikimybės tankio funkcija normaliam skirstiniui su tikėtina vertė 0 ir standartiniu nuokrypiu 1.

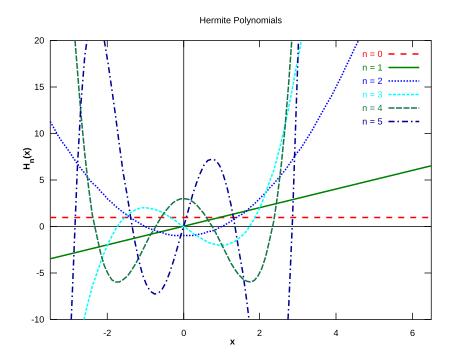Pirmi penki Ermito polinomai.

Pirmi vienuolika Ermito polinomu, apibrėžtų pagal tikimybių teorijoje naudojamą apibrėžimą:

$H_{0}(x)=1\,$

$H_{1}(x)=x\,$

$H_{2}(x)=x^{2}-1\,$

$H_{3}(x)=x^{3}-3x\,$

$H_{4}(x)=x^{4}-6x^{2}+3\,$

$H_{5}(x)=x^{5}-10x^{3}+15x\,$

$H_{6}(x)=x^{6}-15x^{4}+45x^{2}-15\,$

$H_{7}(x)=x^{7}-21x^{5}+105x^{3}-105x\,$

$H_{8}(x)=x^{8}-28x^{6}+210x^{4}-420x^{2}+105\,$

$H_{9}(x)=x^{9}-36x^{7}+378x^{5}-1260x^{3}+945x\,$

$H_{10}(x)=x^{10}-45x^{8}+630x^{6}-3150x^{4}+4725x^{2}-945\,$

ir pirmi vienuolika Ermito polinomu, apibrėžtų pagal fizikoje (kvantinėje mechanikoje) naudojamą apibrėžimą:

$H_{0}(x)=1\,$

$H_{1}(x)=2x\,$

$H_{2}(x)=4x^{2}-2\,$

$H_{3}(x)=8x^{3}-12x\,$

$H_{4}(x)=16x^{4}-48x^{2}+12\,$

$H_{5}(x)=32x^{5}-160x^{3}+120x\,$

$H_{6}(x)=64x^{6}-480x^{4}+720x^{2}-120\,$

$H_{7}(x)=128x^{7}-1344x^{5}+3360x^{3}-1680x\,$

$H_{8}(x)=256x^{8}-3584x^{6}+13440x^{4}-13440x^{2}+1680\,$

$H_{9}(x)=512x^{9}-9216x^{7}+48384x^{5}-80640x^{3}+30240x\,$

$H_{10}(x)=1024x^{10}-23040x^{8}+161280x^{6}-403200x^{4}+302400x^{2}-30240\,$

Taip pat skaitykite

• Gauso pluoštas
• Ermito ir Gauso pluoštas