Bertrano paradoksas
Bertrano paradoksas (arba Bertrano uždavinys[1]) yra problema su klasikine tikimybių teorijos interpretacija. Paradoksas parodo, kad galima gauti skirtingus to paties tikimybių teorijos uždavinio atsakymus, jei atsitiktinį kintamąjį nusakantis mechanizmas nėra aiškiai suformuluotas. Uždavinys yra pavadintas jį suformulavusio matematiko Juozapo Bertrano vardu.
Uždavinys[redaguoti | redaguoti vikitekstą]
Bertrano uždavinys formuluojamas taip: lygiakraštis trikampis (arba trikampis, kurio visos kraštinės yra lygios) yra įbrėžtas į apskritimą. Tarkime, kad yra atsitiktinai parenkama apskritimo styga. Kokia yra tikimybė, kad ta atsitiktinai parinkta styga yra ilgesnė už įbrėžto trikampio kraštinę?
Sprendimai[redaguoti | redaguoti vikitekstą]
Bertranas šį uždavinį išsprendė trimis skirtingais ir, atrodytų, teisingais būdais, kurie pateikia skirtingus atsakymus:[2]
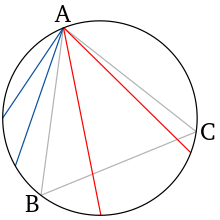
Atsitiktinių stygos galų metodas[redaguoti | redaguoti vikitekstą]
Atsitiktinai pasirenkame tašką apskritimo lanke (arba, kitaip tariant, pakraštyje) ir pasukame įbrėžtą trikampį taip, kad parinktas taškas sutaptų su viena iš jo viršūnių, kurią pažymime raide A. Atsitiktinai pasirenkame dar vieną apskritimo lanko tašką ir tuos du taškus sujungiame. Gauta styga bus ilgesnė tada ir tik tada, kai antrasis atsitiktinai parinktas taškas papuls į lanką tarp trikampio viršūnių B ir C. Kadangi šis lankas užima 1/3 apskritimo lanko ilgio, tikimybė, kad atsitiktinai parinkta styga bus ilgesnė už trikampio kraštinę, yra 1/3.
Atsitiktinio spindulio metodas[redaguoti | redaguoti vikitekstą]

Atsitiktinai parenkame apskritimo spindulį ir pasukame trikampį taip, kad viena iš jo kraštinių būtų statmena parinktam spinduliui. Atsitiktinai parenkame tašką ant spindulio ir nubrėžiame stygą, kuriai parinktas spindulio taškas bus centru (ši styga spinduliui bus statmena). Tokia styga yra ilgesnė už įbrėžto trikampio kraštinę tada ir tik tada, kai atsitiktinai parinktas spindulio taškas yra arčiau apskritimo centro nei taškas, kuriame trikampis susikerta su spinduliu. Kadangi trikampio kraštinė dalija spindulį į dvi lygias dalis, tikimybė, kad atsitiktinai parinkta styga bus ilgesnė už trikampio kraštinę, yra lygi 1/2.
Atsitiktinio vidurio taško metodas[redaguoti | redaguoti vikitekstą]

Atsitiktinai parenkame tašką bet kur apskritime ir nubrėžiame stygą, kuriai tas taškas bus viduriniu. Styga bus ilgesnė už įbrėžto trikampio kraštinę tada ir tik tada, kai ji pateks į apskritimą, kuris yra įbrėžtas į trikampį. Taip yra todėl, kad visos apskritimą liečiančios stygos yra vienodo ilgio, kuris yra lygus trikampio kraštinei, nes ji irgi yra apskritimą liečianti styga. Mažesniojo skritulio plotas yra keturis kartus mažesnis nei didesniojo skritulio, todėl tikimybė, kad atsitiktinai parinkta styga bus ilgesnė už trikampio kraštinę, yra lygi 1/4.
Skirtingų atsitiktinių stygos parinkimų vizualizacijos[redaguoti | redaguoti vikitekstą]
Skirtumai tarp trijų pasirinkimo metodų gali būti parodyti brėžiniais, kurie sudaryti atsitiktinai parinkus didelį kiekį stygų nurodytais metodais. Styga yra unikaliai apibrėžiama nusakant jos vidurio tašką. Kiekvienas iš trijų aprašytų metodų sukuria skirtingą stygų vidurio taškų išsidėstymą skritulyje. Iš brėžinių matome, kad pirmuoju ir antruoju metodais parinktų stygų vidurio taškai yra pasiskirstę po skritulį netolygiai, o trečiuoju (atsitiktinio vidurio taško) metodu - tolygiai. Iš kitos pusės, iš žemiau pateiktų pačių atsitiktinai parinktų stygų grafikų galima matyti, kad antruoju (atsitiktinio spindulio) metodu parinktos stygos nuspalvina skritulį tolygiai, o trečiuoju ir pirmuoju metodu parinktos stygos - netolygiai.
Klasikinis paradokso sprendimas[redaguoti | redaguoti vikitekstą]
Paradoksas rodo, kad tikimybių teorijos uždaviniuose visada reikia tiksliai apibrėžti, ką reiškia žodis „atsitiktinai“. Pasirodo, kad uždavinys turi gerai apibrėžtą atsakymą tik jei yra sukonkretinta, koks atsitiktinio pasirinkimo metodas yra naudojamas. Šiuo atveju uždavinyje nėra nurodytas joks unikalus stygų parinkimo metodas, todėl uždavinys neturi ir unikalaus teisingo sprendimo. Bertrano sprendimo metodų atsakymai kaip tik ir skiriasi dėl skirtingų parinkimo metodų ir jei uždavinyje nėra nurodyta daugiau sąlygų, nėra jokios priežasties vieną iš metodų laikyti geresniu ar teisingesniu už kurį nors kitą. Šis ir kiti klasikinės tikimybės paradoksai privertė matematikus suformuluoti griežtesnius tikimybės apibrėžimus.
Šaltiniai[redaguoti | redaguoti vikitekstą]
- ↑ Jonas Kubilius - Tikimybių teorija ir matematinė statistika (Antras leidimas, 1996 m., Vilniaus Universiteto leidykla)
- ↑ Joseph Louis François Bertrand - Calcul des probabilités {1888 m.)






