Elektrinis laukas

Kitos reikšmės – Laukas (reikšmės).

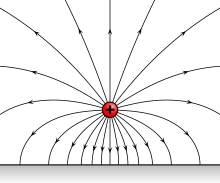
Elektrinis laukas yra materijos forma, supanti krūvius. Kiekvienas krūvis erdvėje aplink save sudaro elektrinį lauką. Visos elektrinių jėgų sąveikos yra perduodamos elektriniu lauku. Nekintantis laike elektrinis laukas yra vadinamas elektrostatiniu lauku.

Elektrinio lauko stipris

Pagrindinė elektrinio lauko charakteristika yra elektrinio lauko stipris (žymimas $\mathbf{E}$). Jis yra lygus jėgai, veikiančiai vienetinį teigiamą krūvį:

$\mathbf{E} = \frac{\mathbf{F}}{q}$.

Stiprio matavimo vienetas pagal SI sistemą yra N/C arba V/m.

El. lauko stipris yra vektorinis dydis. Jo kryptis, esant teigiamam taškiniam krūviui, yra nukreiptas nuo krūvio, o esant neigiamam krūviui – į krūvį.

Taškinio krūvio q sudaryto elektrinio lauko stipris taške, nutolusiame atstumu r nuo to krūvio, gali būti apskaičiuotas pasitelkus Kulono dėsnį:

$\mathbf{E}=\frac{q} {4 \pi \epsilon_0 r^2}\mathbf{\hat{r}}$,

kur $\mathbf{\hat{r}}$ yra vienetinis vektorius.

Superpozicijos principas

Jeigu elektrinį lauką kuria daug taškinių krūvių (sistema), tai šio elektrinio lauko stipris yra lygus atskirų tų sistemos krūvių sukurtų laukų stiprių vektorinei sumai:

$\mathbf{E}=\sum_i \mathbf{E_i}=\frac{1}{4 \pi \epsilon \epsilon_0} \sum_i \frac{q_i}{r_i^2}\mathbf{\hat{r}_i}$

Elektrinio lauko energija

Elektrinio lauko energija tūrio vienete:

$w = \frac{1}{2} \varepsilon |\mathbf{E}|^2$

Elektrinio lauko energija tūryje V:

$W = \int_{V} \frac{1}{2} \varepsilon |\mathbf{E}|^2 \, \mathrm{d}V$

Sūkurinis elektrinis laukas

Sūkurinis elektrinis laukas – kintamojo magnetinio lauko kuriamas elektrinis laukas. Šio lauko stiprio linijos yra uždaros.

$\oint_L \mathbf{E} \cdot \mathrm{d}\mathbf{S} = -\frac{\mathrm{d} \Phi_m} {\mathrm{d} t}$

kur

Φ_m – magnetinės indukcijos srautas.