Konvoliucija
Matematikoje konvoliucija – matematinis operatorius, kuris kaip argumentus paima dvi funkcijas „f“ ir „g“ ir grąžina trečią, kuri, tam tikra prasme, parodo „f“ ir „g“ persidengimo kiekį.
Dažniausiai viena funkcija imama kaip fiksuotas filtras, dar vadinamas branduoliu (angl. kernel).
Apibrėžimas[redaguoti | redaguoti vikitekstą]
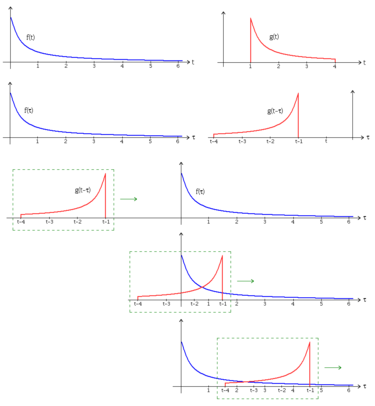
ir funkcijų konvoliucija žymima . Ji apibrėžiama kaip funkcijų sandaugos integralas, po to, kai viena jų buvo paversta ir padauginta iš -1. Taigi, konvoliucija yra integralinės transformacijos rūšis:
Integravimo rėžiai priklauso nuo funkcijų apibrėžimo srities. Dažniausiai a = -∞ ir b = +∞. Integravimo baigtiniame intervale atveju, ir dažnai išplečiamos periodiškai abejomis kryptimis, kad reiškinyje argumentas visada priklausytų apibrėžimo sričiai. Toks periodinis sričių panaudojimas kartais vadinamas cikline arba periodine konvoliucija. Kai apibrėžimo sritis išplečiama, imant funkcijos reikšmes naujuose taškuose lygius 0, konvoliucija vadinama tiesine.
Diskreti konvoliucija[redaguoti | redaguoti vikitekstą]
Diskrečioms funkcijoms galime apibrėžti diskrečią konvoliucijos operaciją:
Naudojant pastarąją formulę konvoliucijos sudėtingumas yra lygus O(N²) aritmetinių operacijų „N“ taškams. Tačiau šis dydis gali būti sumažintas iki O(N log N), panaudojant greitesnius algoritmus.
Greiti konvoliucijos algoritmai[redaguoti | redaguoti vikitekstą]
Praktikoje, skaitmeniniame signalų apdorojime, ir kituose uždaviniuose, kuriuose naudojama diskrečioji konvoliucija, paprastai naudojami greitesni konvoliucijos skaičiavimo algoritmai, sumažinantys sudėtingumą iki O(N log N).
Plačiausiai taikomas greitosios konvoliucijos algoritmas naudoja greitosios Furjė transformacijos algoritmą (angl. FFT) konvoliucijos teoremos pagalba: randama ciklinė konvoliucija imant FFT kiekvienos sekos atskirai, dauginama pataškiui, ir tada atliekama atvirkštinė FFT. Neciklinės konvoliucijos gali būti paskaičiuotos naudojant nulinį išplėtimą.
Žinoma, yra ir kitokių greitosios konvoliucijos algoritmų, nenaudojančių FFT, pavyzdžiui, skaičių teorijos transformacijos algoritmai.
Savybės[redaguoti | redaguoti vikitekstą]
Komutatyvumas[redaguoti | redaguoti vikitekstą]
Asociatyvumas[redaguoti | redaguoti vikitekstą]
Distributyvumas[redaguoti | redaguoti vikitekstą]
Vienetinis elementas[redaguoti | redaguoti vikitekstą]
kur δ žymi δ funkciją.
Daugybos su skaliaru asociatyvumas[redaguoti | redaguoti vikitekstą]
kiekvienam realiam (arba kompleksiniam) .
Diferencijavimo taisyklė[redaguoti | redaguoti vikitekstą]
kur žymi išvestinę, arba, diskrečiu atveju, skirtumo operatorių . Rezultate į konvoliuciją galima žiūrėti kaip į išlyginimo operaciją: „f“ ir „g“ konvoliucija diferencijuojama tiek kartų, kiek daugiausia diferencijuojama viena iš jų.
Konvoliucijos teorema[redaguoti | redaguoti vikitekstą]
Konvoliucijos teorema sako:
kur žymi Furjė transformaciją, o – konstantą, priklausančią nuo specifinės Furjė transformacijos normavimo (pvz., , jeigu ).
Taikymai[redaguoti | redaguoti vikitekstą]
Konvoliucija ir panašios operacijos dažnai sutinkamos daugumoje inžinerijos ir matematikos uždavinių.
- Optikoje daugybė suliejimų aprašoma konvoliucijomis. Šešėlis (pvz., rankos šešėlis ant stalo, kai ranka yra tarp stalo ir šviesos šaltinio) yra konvoliucija daikto formos, kuris meta šešėlį, ir objekto, kuris skleidžia šviesą.
- Skaitmeniniame vaizdų apdorojime konvoliucinis filtravimas vaidina svarbų vaidmenį daugybėje kontūrų atpažinimo ir panašiuose algoritmuose.
- Tiesinėje akustikoje, aidas yra tikrojo garso ir funkcijos, aprašančios, kaip garsas toje aplinkoje atspindimas daiktų, konvoliucija.
- Skaitmeniniame signalų apdorojime dažninis filtravimas gali būti supaprastintas iki dviejų funkcijų konvoliucijos (duomenų ir filtro), kas bus analogiška duomenų ir filtro dauginimui dažnių erdvėje.
Nuorodos[redaguoti | redaguoti vikitekstą]
- http://www.jhu.edu/~signals/convolve/index.html Konvoliucijos vizualizacija (Java apletas).
- http://www.jhu.edu/~signals/discreteconv2/index.html Diskrečių funkcijų vizualizacija (java apletas).


















![{\displaystyle {\mathcal {F}}(f*g)=k\left[{\mathcal {F}}(f)\right]\cdot \left[{\mathcal {F}}(g)\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c51c6a458453c5f3060d2474cc5a4ac64bbda712)



![{\displaystyle {\mathcal {F}}\left[f(x)\right]\equiv \int _{-\infty }^{\infty }f(x)\exp(\pm 2\pi ix\xi )dx}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9787a8279bd73d3764fcf7637152ae993627f9d3)