Sprendimų medžių mokymas
| |
Šį puslapį ar jo dalį reikia sutvarkyti pagal Vikipedijos standartus. Jei galite, sutvarkykite. |
Sprendimų medžio mokymosi metodas naudoja sprendimų medį kaip prognozavimo modelį, kuris sujungia pastabas apie objektą (pavaizduojama šakomis) su išvadomis apie elemento siektina verte (vaizduojama lapais). Tai - vienas iš prognozavimo modeliavimo metodų, naudojamų statistikoje, duomenų išgavime (data-mining) ir mašininiame mokymesi (machine learning). Medžio modeliai, kuriuose priklausomas kintamasis gali įgauti baigtinę reikšmių aibę, yra vadinami klasifikuojančiais medžiais; tokiuose medžiuose lapai vaizduoja klases, o šakos – sutampančias ypatybes, kurios ir priveda į susijusias klases. Sprendimų medžiai, kur priklausomas kintamasis įgauna nuolatines vertes (paprastai tai - realieji skaičiai) yra vadinami regresijos medžiais.
Sprendimų analizėje, sprendimų medis gali būti panaudotas aiškiai ir vizualiai parodyti sprendimus ir kaip tie sprendimai buvo priimti. Duomenų išgavime sprendimų medis aprašo duomenis, tačiau gautas klasifikavimo medis gali būti naudojamas sprendimų priėmimui. Šiame puslapyje bus aprašomi sprendimų medžiai duomenų išgavimo srityje.
Apžvalga[redaguoti | redaguoti vikitekstą]
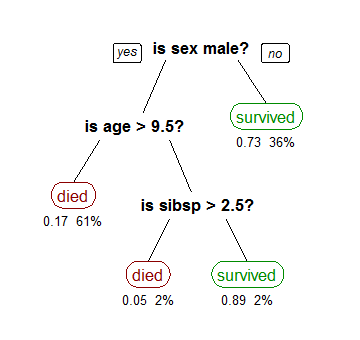
Sprendimų medžio mokymosi metodas yra dažniausiai naudojamas metodas duomenų išgavime.[1] Metodo tikslas - sukurti modelį, kuris prognozuoja priklausomo kintamojo vertę remdamasis keliais nepriklausomais kintamaisiais. Dešinėje schemoje galite pamatyti pavyzdį. Kiekvienas vidinis mazgas atitinka vieną iš nepriklausomų kintamųjų; tiesės keliauja iki pošakių kiekvienam įmanomam nepriklausomo kintamojo variantui. Kiekvienas lapas – tai priklausomo kintamojo reikšmė atsižvelgiant į nepriklausomus kintamuosius, kurie yra pavaizduoti kelyje nuo medžio kamieno iki lapo.
Sprendimų medžio metodas - paprastas klasių pavaizdavimo pavyzdys. Šiame skirsnyje, tarkime, kad visos ypatybės bus imamos iš baigtinės bei diskrečios srities, o išskirtinė norima ypatybė bus vadinama klasifikacija. Kiekvienas klasifikacijos srities elementas bus vadinamas klase. Sprendimų medis (arba klasifikavimo medis) - medis, kuriame kiekvienas vidinis (belapis) mazgas paženklinti tam tikra įvesties ypatybe. Lankai, einantys iš mazgo, pažymėto ta ypatybe, arba žymi visas gautas galimas ypatybes, arba veda prie antraeilio sprendimų mazgo kitai įvesties ypatybei. Visi medžio lapai pažymėti savo klase ar tikimybiniu klasių skirstiniu.

Medis gali būti "išmoktas" padalijant pradinę duotą aibę į poaibius besiremiant elemento verte. Šis procesas kartojamas kiekvienoje gautoje poaibėje grįžtamuoju (rekursiniu) būdu vadinamas rekursiniu dalinimu. Pavyzdžiai parodyti paveikslėlyje: erdvės, kurios nebuvo suskirstytos naudojant rekursinį padalinimu, bei erdvės po rekursinio dvejetainio padalinimo. Dalinimas (rekursija) yra baigtas, kai mazge vaizduojamas poaibis įgauna tą pačią vertę kaip ir priklausomas kintamasis, arba kai tolesnis dalinimas nebeduoda vertės prognozuojant. Ši iš viršaus į apačią vykstanti indukcija sprendimų medžiams (TDIDT [2] – Top-Down Induction of Descision Trees) - gobšaus algoritmo pavyzdys, ir iki šiol išliko labiausiai paplitusi strategija mokantis iš duomenų.
Duomenų išgavimo srityje sprendimų medžiai gali būti apibūdinami, kaip sąjunga tarp matematinių ir skaičiuojamųjų technikų, naudojamų geriau apibūdinti, suskaidyti bei subendrinti duotus duomenis.
Duomenys įrašomi žemiau pavaizduota forma:
Priklausomas kintamasis Y, yra tas kintamasis, kurį mes bandome suprasti, suklasifikuoti arba subendrinti. Vektorius x yra sudarytas iš nepriklausomų kintamųjų, naudojamų šiai užduočiai, - x1, x2, x3, ir t. t.
Tipai[redaguoti | redaguoti vikitekstą]
Sprendimų medžiai, naudojami duomenų išgavime, yra dviejų pagrindinių tipų:
- Klasifikavimo medžio analize vadinama, kai prognozuojama baigtis yra klasė, kuriai duomenys ir priklauso.
- Regresijos medžio analizė - kai prognozuojamas rezultatas gali būti laikoma realiu skaičiumi (pavyzdžiui, namo kaina, arba paciento gulėjimo ligoninėje dienų skaičius).
Terminas Klasifikavimo ir Regresijos Medžio (CART – Classification And Regression Tree) analizė - terminas, pirmąkart pavartotas Breiman bei kolegų[3] yra vartojamas kalbant apie abi anksčiau minėtas procedūras. Medžiai, naudojami regresijai, ir medžiai, naudojami klasifikavimui turi tam tikrų panašumų, tačiau taip pat ir tam tikrų skirtumų, pavyzdžiui, padalinimo tvarkos procedūra.[3]
Kai kurie metodai, dažnai vadinami sambūrio (ensemble) metodais, sukonstruoja daugiau nei vieną sprendimų medį:
- Bagging sprendimų medis (Bootstrap aggregating) - anksti pradėtas naudoti sambūrio metodas – sudaro kelis sprendimų medžius pakartotinai sukaitaliodamas mokymo duomenis su pakaitiniais ir vesdamas medžius ties sutampančia prognoze. [4]
- Atsitiktinis miško klasifikatorius (random forest classifier) naudoja sprendimo medžių skaičių, siekdamas pagerinti klasifikavimo lygį.
- Išpūstų medžių metodas (boosted trees) gali būti naudojamas regresijos ir klasifikacijos tipų problemas spręsti.[5][6]
- Sukimosi miškas – kur kiekvienas sprendimų medis apmokomas pradžioj taikant pagrindinių komponentų analizę (PCA – Principal Components Analysis) įvesties ypatybių atsitiktinės atrankos pogrupyje.[7]
Ypatingas sprendimų medžio atvejis - sprendimų sąrašas,[8] kuris yra vienpusis sprendimų medis, kur kiekvienas vidinis mazgas turi lygiai 1 lapų mazgą ir tiksliai 1 vidaus pomazgį (išskyrus apatinį mazgą, kurio pomazgis - vieno lapo mazgas). Nors mažiau išraiškingi, sprendimų sąrašai - neabejotinai lengviau suprantami nei bendrieji sprendimų medžiai dėl jų pridėto retumo, galimybės naudotis negobšiais mokymosi metodais[9] ir taikomiems monotoniškiems suvaržymams.[10]
Sprendimų medžio mokymasis - sprendimų medžio klasėmis pažymėto mokymo imties statyba. Sprendimų medis turi į srauto diagramą panašią struktūrą, kurioje kiekvienas vidinis (belapis) mazgas parodo požymio bandymą, kiekviena šaka reprezentuoja bandymo rezultatus, ir kiekvienas lapo (ar terminalo) mazgas turi klasės etiketę. Viršutinis mazgas medyje yra kamieninis mazgas.
Yra daug konkrečių sprendimų medžių algoritmų. Žymiausi yra:
- ID3 (Kartotinis Dichotomiser 3)
- C4.5 (ID3 įpėdinis)
- CART (Klasifikavimo Ir Regresijos Medis (CART – Classification And Regression Tree))
- CHAID (automatinis chi-kvadrato sąveikos detektorius (CHi-squared Automatic Interaction Detector)). Sudarant sprendimų medžius atlieka kelių lygių dalinimą.[11]
- MARS: ištęsia sprendimų medžio metodą, kad būtų galima lengviau tvarkyti kiekybinius duomenis.
- Sąlyginės išvados medžiai. Statistika pagrįstas požiūris, kuris naudoja neparametrinius testus, kaip dalinimo kriterijų, pakoreguotą daugeliui bandymų, kad būtų galima išvengti per aukšto kompleksiškumo. Šis požiūris lemia objektyviai prognozuojamas atrankas ir nereikalauja genėjimo.[12][13]
ID3 ir CART buvo išrasti nepriklausomai vienas nuo kito maždaug tuo pačiu laiku (tarp 1970 ir 1980), tačiau abu laikosi panašios strategijos dėl sprendimų medžio mokymo iš apmokymų imties.
Metrikos, skaičiavimai[redaguoti | redaguoti vikitekstą]
Sprendimų medžių konstravimo algoritmai paprastai veikia iš viršaus į apačią kiekviename žingsnyje pasirenkant tokį kintamąjį, kuris padalintų elementų rinkinį geriausiu būdu.[14] Įvairūs algoritmai naudoja skirtingus skaičiavimo būdus (metrikas) matuojant "geriausius" padalinimus - paprastai poaibėje išmatuojamas priklausomų kintamųjų homogeniškumas (pavyzdžiai pateikti žemiau). Šios metrikos taikomos kiekvienam galimam poaibiui, o susidarančios vertės sukombinuojamos (pvz., suvidurkintos) pateikiant padalijimo kokybės matą.
Gini priemaiša[redaguoti | redaguoti vikitekstą]
Naudojamas CART (klasifikavimo ir regresijos medžio) algoritme, Gini priemaiša (Gini impurity)– priemonė apskaičiuoti, kaip dažnai atsitiktinai iš rinkinio pasirinkti elementai būtų neteisingai suženklinti, jei jie buvo atsitiktinai ženklinami pagal etikečių pasiskirstymą pogrupyje. Gini priemaiša gali būti apskaičiuota sudedant elemento tikimybę būti pasirinktam kart tikimybė , kad tas elementas bus sukategorizuotas neteisingai. Gini priemaišos indeksas pasiekia savo minimumą (nulis), kai visų mazgų atvejai patenka į vieną tikslinę kategoriją.
Gini priemaišos elementų aibei su klasių skaičiumi apskaičiuoti, kur , o – elementų, pažymėtu klase duotoje aibėje, funkcija, naudokite
Informacijos išlošis[redaguoti | redaguoti vikitekstą]
Šis metodas naudojamas ID3, C4.5 bei C5.0 medžių generavimo algoritmuose. Informacijos išlošis (Information gain) yra paremtas entropijos samprata, naudojama informacijos teorijoje.
- kur – trupmenos, reprezentuojančios kiekvienos klasės egzistavimo pomazgyje, gauto po medžio išsišakojimo, procentą, ir jos susideda į 1. [15]
Informacijos išlošis = Entropija (prieš) – Suskaičiuota Entropijų Suma (Pomazgyje)
Informacijos išlošis naudojamas nustatant, kokia ypatybė skelia medį kiekviename žingsnyje. Paprastumas yra labiausiai vertinamas, tad tikslas – išlaikyti medį kuo mažesnį, o kad taip įvyktų, reikia medį iššakoti į kuo tikslesnius pomazgius. Dažnai tikslumui nustatyti naudojamas būdas – informacija (matuojama bitais), kuri neturėtų būti maišoma su kompiuterine atmintimi. Kiekvienam medžio mazgui, informacijos vertė reprezentuoja trokštamą informacijos kiekį, kuris yra reikiamas norint nurodyti, ar naujas pavyzdys turėtų būti klasifikuojamas teigiamai ar neigiamai, žinant, kad pavyzdys pasiekė mazgą.[16]
Tarkime, jog turime duomenų su keturiomis ypatybėmis: apžvalga (saulėta, vėjuota, lyja), temperatūra (karšta, vidutinė, šalta), drėgnumas (aukštas, normalus), vėjuotumas (didelis, mažas), pavyzdį, su dvinariu (taip arba ne) priklausomu kintamuoju, 14 duomenų taškų bei atsitikimais. Tam, kad pagal šiuos duomenis sukonstruotume sprendimų medį, reikia palyginti keturių medžių, kiekvieno padalintų pagal vieną iš keturių ypatybių, informacijos išlošius. Padalinimas, turintis didžiausia informacijos išlošį, yra priimamas kaip tikrasis padalinimas, o procesas toliau vykdomas tol, kol visi pomazgiai yra gryni (tikslūs), arba kol informacijos išlošis tampa lygus 0.
Padalijimas pagal ypatybę vėjuotumas duoda du pomazgius, vienas skirtas dideliam vėjuotumui, kitas mažam. Šioje duomenų aibėje, yra šeši duomenų taškai su vejuotumo verte, trys su teigiama atsitikimo verte bei trys su neigiama atsitikimo verte. Aštuoni likę duomenų taškai, kurių vėjuotumo vertė yra maža turi du neigiamus atsitikimus ir šešis teigiamus. Didelio vėjuotumo mazgo informacija apskaičiuojama naudojant aukščiau pateiktą entropijos lygtį. Kadangi yra lygus teigiamų ir neigiamų atsitikimų skaičius, turime:
Mažo vėjuotumo mazge turime 8 duomenų taškus – 6 taip ir 2 ne, tad:
Kad galėtume rasti padalinimo informaciją, imame numerių, paskaičiuotų pagal tai, kiek stebinių patenka į kiekvieną mazgą, vidurkį.
Kad galėtume rasti informacijos išlošį padalinimui pagal vėjuotumą, paskaičiuojama duomenų informaciją prieš dalinimą. Pradiniai duomenys turėjo 9 teigiamus bei 5 neigiamus atsitikimus.
Dabar galima apskaičiuoti informacijos išlošį, gautą po padalinimo pagal vėjuotumą.
Norint sukonstruoti medį, turi būti suskaičiuotas kiekvieno įmanomo pirmojo padalinimo informacijos išlošis. Geriausias pirmasis dalinimas – tas su didžiausiu informacijos išlošiu. Procesas tuomet kartojamas kiekvienam negrynam (netiksliam) mazgui, kol užbaigiamas medis. Šis pavyzdys pritaikytas iš pavyzdžio, parodyto Witten bei kolegų darbe.[17]
Variacijos sumažinimas[redaguoti | redaguoti vikitekstą]
Pirmąkart panaudotas CART metode,[3] variacijos sumažinimas dažnai naudojamas situacijose kai priklausomas kintamasis yra tolydus (regresijos medis), kadangi naudojantis daugeliu kitų metrikų pradžioje reikalauja diskretizavimo išpildymo. Mazgo variacijos sumažinimas yra aprašomas, kaip visas priklausomo kintamojo variacijos sumažinimas šio mazgo dalinime.
kur – aibė, sudaryta iš dalinimo indeksų imties prieš dalinimą, -aibė, sudaryta iš dalijimo indeksų imties, kur dalinimo testas teigiamas, bei – aibė, sudaryta iš dalinimo indeksų imties po dalinimo, kur dalinimo testas neigiamas. Apibūdinti dydžiai reikalingi nustatant variaciją nors ir yra surašyti taip, kad tiesiogiai nenurodo vidurkio.
Sprendimų medžių privalumai[redaguoti | redaguoti vikitekstą]
Tarp visų kitų metodų duomenų išgavime, sprendimo medžiai turi įvairių privalumų:
- Paprasta suprasti ir interpretuoti. Žmonės jau po trumpų paaiškinimų sugeba juos suprasti. Medžiai taip pat gali būti pavaizduojami grafiškai, tad net ir nepatyrusiems asmenims tampa lengva juos interpretuoti. [18]
- Susidoroja tiek su skaitiniais tiek su kategoriniais duomenimis. [18] Kiti metodai labiau sutelkti ties vieno kintamojo tipo duomenimis (pavyzdžiui, sąryšio taisyklės naudojamos tik su nominaliais kintamaisiais, kai neuroniniai tinklai naudojami tik su skaitiniais kintamaisiais).
- Nereikalauja daug duomenų ruošimo. Kiti metodai dažnai reikalauja duomenų normalizavimo. Kadangi medžiai veikia su kokybiniais faktoriais, nėra prasmės naudoti fiktyviųjų kintamųjų.[18]
- Naudoja „baltosios dėžės“ modelį. Jei duota situacija atsispindi modelyje, sąlygą lengva paaiškinti naudojant Boolean logiką (Boolean logic). Palyginant, „juodosios dėžės“ modelyje dažnai tampa sunku paprastai paaiškinti sąlygą, kaip ir yra su dirbtiniais neuroniniais tinklais.
- Galima patikrinti modelį naudojant statistinius testus, o tai modeliui prideda daug patikimumo.
- Patikimas. Puikiai dirba net ir prielaidos pažeidžiamos tikrojo modelio, iš kurio duomenys buvo sugeneruoti.
- Puikiai tinka didelėms duomenų apimtims. Didelės duomenų apimtys gali būti apdorojamos įprastais kompiuteriniais ištekliais bei per priimtiną laiką.
- Atvaizduoja žmogaus sprendimų eigą tikroviškiau, nei kiti metodai.[18] Tai labai patogu analizuojant žmonių elgesį.
Apribojimai, suvaržymai[redaguoti | redaguoti vikitekstą]
- Medžiai ne tokie tikslūs kaip kiti metodai. [18]
- Yra atvejų, kai jie tampa labai nepatikimi. Mažas pokytis mokymo imtyje gali reikšti didelį pokytį medžio struktūroje bei esminiuose spėjimuose.[18]
- Optimalių sprendimų medžių mokymo problema žinoma yra kaip NP-užbaigta kai kuriais optimalumo bei paprastais aspektais.[19][20] Dėl to praktinis sprendimų medžio algoritmas yra paremtas tokiomis euristikomis, kaip „smalsusis algoritmas“ (Greedy algorithm), kur lokaliai optimalūs sprendimai priimami kiekviename mazge.Tokie algoritmai negali garantuoti globaliai optimalaus gaunamo sprendimų medžio. Norint sumažinti lokalaus optimalumo godumo efektą buvo pasiūlyti metodai, tokie kaip dvejopas informacijos atstumas (DID – dual information distance).[21] [1] Archyvuota kopija 2016-06-04 iš Wayback Machine projekto.
- Sprendimų medžio mokymas gali sukurti per sudėtingus medžius, kurie aiškiai nesubendrins mokymo imties (tai dar žinoma kaip perspaudimas (overfitting[22])). Metodai, kaip medžio genėjimas, tampa reikalingi norint išvengti šios problemos (su kai kurių algoritmų, kaip sąlyginių išvadų metodas, kuris nereikalauja genėjimo, išimtimi.[12][13])
- Kai kurias sąvokas sunku išmokti, kadangi sprendimų medžiai jų aiškiai neparodo, tarkim XOR, lyginumo ar daugiklio problemos. Tokiais atvejais sprendimų medis tampa pernelyg didelis., o šios problemos sprendimas įtraukia problemos esmės pakeitimą (žinomą kaip siūlymavimas (propositionalization[23] )) arba algoritmų, paremtų išraiškingesnėmis reprezentacijomis (kaip statistinis sąryšių mokymasis ar induktyvus loginis programavimas), naudojimas.
- Kategorinių kintamųjų su skirtingais lygių skaičiais duomenims sprendimų medžių informacijos išlošis yra šališkas ypatybių su daugiau lygių naudai.[24] Tačiau ši problema aplenkiama sąlyginių išvadų metodu.[12]
Plėtiniai[redaguoti | redaguoti vikitekstą]
Sprendimų grafikai[redaguoti | redaguoti vikitekstą]
Sprendimų medžiuose keliai nuo kamieno iki lapų mazgų eina jungtukiniu būdu, arba IR. Sprendimų grafikuose galima naudoti ir skirtinius (ARBA), sujungiant du ar daugiau kelių, naudojant minimalaus žinutės ilgio metodą (MML- minimum message length).[25] Sprendimų grafikai buvo dar išplėsti tam, kad leistų dinamiškai išmokti anksčiau neįvardintas naujas ypatybes bei jas naudoti skirtingose grafikų vietose.[26] Bendrinės schemos kūrimas duoda didesnį spėjimo tikslumą bei logaritminį tikimybinį skaičiavimą. Apskritai, sprendimų grafikai išveda medžius su mažiau lapų, nei sprendimų medžiai.
Alternatyvūs paieškos metodai[redaguoti | redaguoti vikitekstą]
Bandant išvengti lokalių optimalių sprendimų bei rasti sprendimų medžių erdvę su mažu išankstiniu nusistatymu, buvo pasiūlyti novatoriški algoritmai.[27][28]
Medžiui taip pat įmanoma naudoti MCMC imtį.[29]
Medis gali būti apieškomas ir iš apačios į viršų.[30]
Vykdymas[redaguoti | redaguoti vikitekstą]
Daugelis duomenų išgavimo programinių paketų duoda vieno ar kito sprendimų medžio algoritmo vykdymą. Verti paminėjimo yra Salford Systems CART (kurie turi originaliems CART autoriams priklausomo kodo licenciją,[3] IBM SPSS Modeler, RapidMiner, SAS Enterprise Miner, Matlab, R (atviro kodo statistinių skaičiavimų programinė įranga, turinti kelis CART skaičiavimo vykdymus, tokius kaip rpart, party bei randomForest paketus), Weka (nemokamas atviro kodo duomenų išgavimo rinkinys), Orange (nemokamas duomenų išgavimo mašininio mokymo rinkinys, įtraukiantis ir medžių modulį orngTree), KNIME, Microsoft SQL Server [2]bei scikit-learn (nemokama atviro kodo mšininio mokymo biblioteka Python programavimo kalbai).
Šaltiniai[redaguoti | redaguoti vikitekstą]
- ↑ Rokach, Lior; Maimon, O. (2014). Data mining with decision trees: theory and applications, 2nd Edition. World Scientific Pub Co Inc. doi:10.1142/9097. ISBN 978-9814590075. S2CID 44697571.
- ↑ Quinlan, J. R., (1986). Induction of Decision Trees. Machine Learning 1: 81-106, Kluwer Academic Publishers
- ↑ 3,0 3,1 3,2 3,3 Breiman, Leo; Friedman, J. H.; Olshen, R. A.; Stone, C. J. (1984). Classification and regression trees. Monterey, CA: Wadsworth & Brooks/Cole Advanced Books & Software. ISBN 978-0-412-04841-8.
- ↑ Breiman, L. (1996). Bagging Predictors. "Machine Learning, 24": pp. 123-140.
- ↑ Friedman, J. H. (1999). Stochastic gradient boosting. Stanford University.
- ↑ Hastie, T., Tibshirani, R., Friedman, J. H. (2001). The elements of statistical learning : Data mining, inference, and prediction. New York: Springer Verlag.
- ↑ Rodriguez, J.J. and Kuncheva, L.I. and Alonso, C.J. (2006), Rotation forest: A new classifier ensemble method, IEEE Transactions on Pattern Analysis and Machine Intelligence, 28(10):1619-1630.
- ↑ Rivest, Ron (Nov 1987). „Learning Decision Lists“ (PDF). Machine Learning. 3 (2): 229–246. doi:10.1023/A:1022607331053.
- ↑ Letham, Ben; Rudin, Cynthia; McCormick, Tyler; Madigan, David (2015). „Interpretable Classifiers Using Rules And Bayesian Analysis: Building A Better Stroke Prediction Model“. Annals of Applied Statistics. 9: 1350–1371. arXiv:1511.01644. doi:10.1214/15-AOAS848.
- ↑ Wang, Fulton; Rudin, Cynthia (2015). „Falling Rule Lists“ (PDF). Journal of Machine Learning Research. 38. Suarchyvuotas originalas (PDF) 2016-01-28. Nuoroda tikrinta 2016-12-22.
- ↑ Kass, G. V. (1980). „An exploratory technique for investigating large quantities of categorical data“. Applied Statistics. 29 (2): 119–127. doi:10.2307/2986296. JSTOR 2986296.
- ↑ 12,0 12,1 12,2 Hothorn, T.; Hornik, K.; Zeileis, A. (2006). „Unbiased Recursive Partitioning: A Conditional Inference Framework“. Journal of Computational and Graphical Statistics. 15 (3): 651–674. doi:10.1198/106186006X133933. JSTOR 27594202.
- ↑ 13,0 13,1 Strobl, C.; Malley, J.; Tutz, G. (2009). „An Introduction to Recursive Partitioning: Rationale, Application and Characteristics of Classification and Regression Trees, Bagging and Random Forests“. Psychological Methods. 14 (4): 323–348. doi:10.1037/a0016973.
- ↑ Rokach, L.; Maimon, O. (2005). „Top-down induction of decision trees classifiers-a survey“. IEEE Transactions on Systems, Man, and Cybernetics, Part C. 35 (4): 476–487. doi:10.1109/TSMCC.2004.843247.
- ↑ Witten, Ian; Frank, Eibe; Hall, Mark (2011). Data Mining. Burlington, MA: Morgan Kaufmann. pp. 102-103. ISBN 978-0-12-374856-0.
- ↑ Witten, Ian; Frank, Eibe; Hall, Mark (2011). Data Mining. Burlington, MA: Morgan Kaufmann. pp. 102-103. ISBN 978-0-12-374856-0.
- ↑ Witten, Ian; Frank, Eibe; Hall, Mark (2011). Data Mining. Burlington, MA: Morgan Kaufmann. pp. 102-103. ISBN 978-0-12-374856-0.
- ↑ 18,0 18,1 18,2 18,3 18,4 18,5 Gareth, James; Witten, Daniela; Hastie, Trevor; Tibshirani, Robert (2015). An Introduction to Statistical Learning. New York: Springer. p. 315. ISBN 978-1-4614-7137-0.
- ↑ Hyafil, Laurent; Rivest, RL (1976). „Constructing Optimal Binary Decision Trees is NP-complete“. Information Processing Letters. 5 (1): 15–17. doi:10.1016/0020-0190(76)90095-8.
- ↑ Murthy S. (1998). Automatic construction of decision trees from data: A multidisciplinary survey. Data Mining and Knowledge Discovery
- ↑ Ben-Gal I. Dana A., Shkolnik N. and Singer (20). „Efficient Construction of Decision Trees by the Dual Information Distance Method“ (PDF). Quality Technology & Quantitative Management (QTQM), 11( 1), 133-147. Suarchyvuotas originalas (PDF) 2016-06-04. Nuoroda tikrinta 2016-12-22.
{{cite journal}}: Citatai journal privalomas|journal=(pagalba); Patikrinkite date reikšmes:|year=(pagalba) - ↑ „Principles of Data Mining“. 2007. doi:10.1007/978-1-84628-766-4. ISBN 978-1-84628-765-7.
{{cite journal}}: Citatai journal privalomas|journal=(pagalba) - ↑ Horváth, Tamás; Yamamoto, Akihiro, eds. (2003). „Inductive Logic Programming“. Lecture Notes in Computer Science. 2835. doi:10.1007/b13700. ISBN 978-3-540-20144-1.
{{cite journal}}: Citatai journal privalomas|journal=(pagalba) - ↑ Deng,H. (2011). "Bias of importance measures for multi-valued attributes and solutions" in Proceedings of the 21st International Conference on Artificial Neural Networks (ICANN). {{{booktitle}}}: 293–300.
- ↑ http://citeseer.ist.psu.edu/oliver93decision.html
- ↑ Tan & Dowe (2003)
- ↑ Papagelis A., Kalles D.(2001). Breeding Decision Trees Using Evolutionary Techniques, Proceedings of the Eighteenth International Conference on Machine Learning, p.393-400, June 28-July 01, 2001
- ↑ Barros, Rodrigo C., Basgalupp, M. P., Carvalho, A. C. P. L. F., Freitas, Alex A. (2011). A Survey of Evolutionary Algorithms for Decision-Tree Induction. IEEE Transactions on Systems, Man and Cybernetics, Part C: Applications and Reviews, vol. 42, n. 3, p. 291-312, May 2012.
- ↑ Chipman, Hugh A., Edward I. George, and Robert E. McCulloch. "Bayesian CART model search." Journal of the American Statistical Association 93.443 (1998): 935-948.
- ↑ Barros R. C., Cerri R., Jaskowiak P. A., Carvalho, A. C. P. L. F., A bottom-up oblique decision tree induction algorithm. Proceedings of the 11th International Conference on Intelligent Systems Design and Applications (ISDA 2011).
Nuorodos[redaguoti | redaguoti vikitekstą]
- Statybos Sprendimų Medžiai "Python" programavimo kalba Archyvuota kopija 2011-08-07 iš Wayback Machine projekto. Iš O' Reilly.
- Papildymas "Statybos Sprendimų Medžiai "Python" programavimo kalba" Iš O' Reilly.
- Sprendimų Medžiai Pamoka naudojant "Microsoft Excel".
- Sprendimų Medžiai puslapyje aitopics.orgpuslapis su komentavo nuorodos.
- Sprendimų medis įgyvendinimo Ruby (AI4R)
- Evoliucijos Mokymosi Sprendimo Medžių C++
- "Java" įgyvendinimo Sprendimų Medžiai remiantis Informacija Pelnas
- Labai aiškų paaiškinimą, informaciją įgyti kuo skaldymo kriterijus











![{\displaystyle I_{E}([3,3])=-(3/6)\log _{2}^{}(3/6)-(3/6)\log _{2}^{}(3/6)=-(1/2)\log _{2}^{}(1/2)-(1/2)\log _{2}^{}(1/2)=1}](https://wikimedia.org/api/rest_v1/media/math/render/svg/2667ace0df84c09d05bf855e08556b7109c21fff)
![{\displaystyle I_{E}([6,2])=-(6/8)\log _{2}^{}(6/8)-(2/8)\log _{2}^{}(2/8)=-(3/4)\log _{2}^{}(3/4)-(1/4)\log _{2}^{}(1/4)=0.8112781}](https://wikimedia.org/api/rest_v1/media/math/render/svg/36c88fd7c35767082432916d10b3ed4c7f535fab)

![{\displaystyle I_{E}([9,5])=-(9/14)\log _{2}^{}(9/14)-(5/14)\log _{2}^{}(5/14)=0.940286}](https://wikimedia.org/api/rest_v1/media/math/render/svg/471ca8e64656904b90c9daedf05645e3e5dfb183)
![{\displaystyle IG(vejuotumas)=I_{E}([9,5])-I_{E}([3,3],[2,6])=0.940286-0.8921589=0.0481271}](https://wikimedia.org/api/rest_v1/media/math/render/svg/b589d55a8734c82830717df0f89715f8d4739af3)





