Fazė
| |
Manoma, kad šis straipsnis yra beviltiškas. Jo turinys, struktūra, stilius ar kitos savybės yra tokios, kad jo neįmanoma pritaikyti enciklopedijai. Priežastis atskirai nesukonkretinta, bet jei ji neakivaizdi, tai gali būti nurodyta istorijoje ar aptarime. Jei galite parašyti šį straipsnį iš naujo, tegul ir kelis kartus mažesnį, taip ir padarykite! |
Sąvoka fazė bangų fizikoje yra susijusi su aprašomo kompleksiniais kintamaisiais fizikinio dydžio matematiniu atvaizdavimu. Fazė yra kampas, kurį sudaro fizikinį dydį kompleksinėje plokštumoje vaizduojantis vektorius su realiųjų skaičių ašimi. Kuomet fizikinis dydis kinta laike arba erdvėje, kinta jį aprašantis kompleksinis skaičius. Kuomet kinta kampas tarp kompleksinio dydžio vektoriaus ir realiųjų skaičių ašies, tuomet kinta ir fizikinio dydžio fazė. Jei fizikino dydžio fazės kitimas yra tiesinis laikui begant arba padėčiai besikeičiant, tuomet fizikoje yra kalbama apie harmoninę fizikinio dydžio priklausomybę, nes pagal Oilerio formulę kompleksinio argumento eksponentė yra atskiriama į realią ir menamą dalis, aprašomas trigonometrinėmis funkcijomis. Fazės sąvoka yra lengviau suvokti nagrinėjant elementarius atsikartojančius procesus, aprašomus paprastomis sinuso arba kosinuso funkcijomis. Šiuo atveju fazė yra periodinio vyksmo ciklo dalis, atitinkanti tam tikrą dydžio pokytį, įvykusį nuo proceso stebėjimo pradžios t = 0.
Fazės sąvoka taip pat plačiai naudojama signalų analizėje nagrinėjant dažninės signalo charakteristikas,[1][2] gaunamas atlikus signalą aprašančio dydžio Furjė transformaciją. Fazės sąvoka yra intuityvi signalų spektriniame nagrinėjime, kadangi Furjė transformacijos rezultatas gali būti interpretuotas kaip signalą sudarančių trigonometrinių funkcijų kompleksinių amplitudžių nustatymas. Ši procedūra leidžia sudėtingiausią signalą nagrinėti, kaip atskyrų harmoninių svyravimų sumą - bangų interferencija. Ta pati metodika gali būti taikoma net tik laike kintantiems signalams, bet ir erdvėje. Elementaraus harmoninio proceso pavyzdys gali būti stygos svyravimas, kuomet laike kinta stygos taško padėtis, arba kinta stygos aukštis erdvėje:
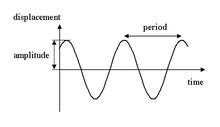
ir yra aprašomas formule:
kur A yra svyravimo amplitudė, f yra dažnis. Dažnio f virpesys turi periodą yra nuo stebėjimo pradžios praėjęs laikas, o dydis yra svyravimo pradinė fazė. Ji aprašo pradinį stygos taško poslinkį nuo pusiausvyros padėties stebėjimo pradžios momentu t = 0. Reiškinys po sinuso argumentu yra bendroji fazė.
Kuomet kalbama apie fazę dažnai reiškinio supratime kyla problemos dėl skirtumų naudojamuose apibrėžimuose :
- Pakeitus svyravimo apibrėžime sinuso funkcija į kosinuso, pradinis stygos poslinkis bus kitokios vertės, nors pradinė fazė bus ta pati.
- Nuo laiko priklausantis trigonometrinės funkcijos argumentas (kampas) arba dydžio modulis pagrindu , dažnai sutrumpintai vadinamas fazė.
Fazės poslinkis[redaguoti | redaguoti vikitekstą]

Pradinė fazė taip pat vadinama fazės poslinkiu, kadangi ji atitinka argumento prieaugį nuo nulinės fazės vertės. Taip pat ši sąvoka būna vartojama pokyčių dydyje apibrėžti.
Pakankamai ilgiems laiko tarpams pokytis dydyje atitinka poslinkį laike - delsą. Jei yra uždelsiama (pastumiama laike) per nuo ciklo pradžios, priklausomybė tampa:
kur jos "nauja" fazė dabar yra Duotu atveju fazė buvo paslinkta per .
Fazių skirtumas[redaguoti | redaguoti vikitekstą]



Sakoma, kad du svyravimai, vykstantis tuo pačiu dažniu, bet turintys skirtingas pradines fazes, turi fazių skirtumą, o svyravimai yra išfazuoti. Šis fazių skirtumas gali būti išreiškiamas laipsniais ir įgija vertes nuo 0° iki 360°; kuomet naudojami radianai, jo vertė kinta nuo 0 iki 2π. Kuomet fazių skirtumas yra 180 laipsnių (π radianų), tuomet svyravimai vyksta priešfazėje. Kuomet dvi vienodo dažnio bangos kažkuriame erdvės taške arba kažkurio laiko momentu yra priešfazėje, tuomet įvyksta destruktyvi interferencija ir tame taške fizikinio dydžio vertė yra lygi amplitudžių skirtumui. Fizikoje dažna situacija, kuomet terpėse sklinda vienodo dažnio, bet skirtingų fazių bangos. Fazių skirtumas nulemia tai, kaip bangos interferuos tarpusavyje - ar jos sustiprins viena kitą, ar jos nuslopins viena kitą. Vienodų amplitudžių bangų destruktyvi interferencija sąlygoja bendra amplitudę lygia nuliui. Tuo būdu, fazės reikšme interferencijoje yra panaši į potencialą elektrostatikoje - svarbi yra ne absoliuti reikšmė, bet reikšmių skirtumas.
Pavyzdžiui, Žemės sukimasis yra periodinis procesas. Praktinę reikšmę turi ne absoliuti kampo vertė nuo Žemės sukimosi pradžios, o kampų skirtumai, kuriuos įprasta išreikši laiko vienetais. Fazių skirtumai šiuo atveju taip pat atitinka skirtingas laiko juostas.















