Medis (duomenų struktūra)
| |
Šiam straipsniui ar jo daliai trūksta išnašų į patikimus šaltinius. Jūs galite padėti Vikipedijai pridėdami tinkamas išnašas su šaltiniais. |
 Kitos reikšmės – Medis (reikšmės).
Kitos reikšmės – Medis (reikšmės).
Medžiai – hierarchinės duomenų struktūros, juose tarp medžio elementų egzistuoja „tėvų - vaikų“ santykiai. Kiekvienas elementas yra susietas su vienu ar daugiau elementų. Medžio elementai yra vadinami medžio viršūnėmis. Kitaip nei gamtoje, ši duomenų struktūra dažniausiai vaizduojama iš viršaus į apačią, kai aukščiau esanti viršūnė vadinama tėvu. Elementas, kuris neturi tėvo, vadinamas šaknimi ar šakniniu elementu. Elementai neturintys vaikų vadinami lapais. Viršūnės, kurios nėra lapai, dar vadinamos vidinėmis viršūnėmis.
Medžio aukščiu vadinamas atstumas nuo šaknies iki toliausiai esančio lapo. Medžio viršūnės lygis nusako jos eilės tvarką skaičiuojant nuo šaknies (šaknis yra 0 lygio, jos vaikas 1…).
Dvejetainiai medžiai[redaguoti | redaguoti vikitekstą]
Dvejetainis medis (binary tree) – tai toks medis, kurio kiekviena viršūnė turi ne daugiau kaip 2 vaikus, kurie vadinami dešiniuoju ir kairiuoju medžio pomedžiu.
- Pilnas (full)
- dvejetainis medis, kurio visos viršūnės arba neturi vaikų, arba jų turi 2.
- Tobulas (perfect)
- dvejetainis medis, kuriuo visi lapai yra viename aukštyje
- Užbaigtas (complete)
- tobulas dvejetainis medis. Ši sąvoka yra kartais naudojama pilnam medžiui, kurio lapai yra arba h arba h -1 aukštyje, apibrėžti
Pilnas h aukščio medis turi 2h-1 viršūnių, o bet kuris h aukščio dvejetainis medis turi ne daugiau nei 2h-1 viršūnių. Atitinkamai N viršūnių dvejetainių medžių minimalus aukštis yra .
Dvejetainis paieškos medis[redaguoti | redaguoti vikitekstą]
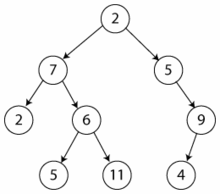
Dvejetainis paieškos medis (binary search tree) – tai dvejetainis medis, kuris surūšiuotas pagal reikšmes jo viršūnėse. Kiekvienai viršūnei jis tenkina tokias tris savybes:
- n-osios viršūnės reikšmė yra didesnė už visas reikšmes jos kairiajame pomedyje.
- n-osios viršūnės reikšmė yra mažesnė už visas reikšmes jos dešiniajame pomedyje.
- Kairysis ir dešinysis pomedžiai yra dvejetainiai paieškos medžiai.
Pasukimas[redaguoti | redaguoti vikitekstą]
Medžio pasukimas tai operacija dvejetainiame paieškos medyje, skirta pakeisti viršūnių padėtį, nepažeidžiant medžio savybių. Yra du operacijos tipai: pasukimas į kairę ir į dešinę. Atliekant pasukimą viena medžio viršūnė kyla, kita – leidžiasi. Dažniausiai ši operacija reikalinga pomedžių aukščiams pakeisti.
Pavyzdžiui, jei turėtume tokį medį:
D
/ \
/ \
B E
/ \
A C
jis galėtų būti pasuktas ir atrodyti taip:
B
/ \
/ \
A D
/ \
C E
Tai būtų pasukimas į dešinę. Jei norėtume iš antro medžio pereiti prie pirmo, reikėtų atlikti pasukimą į kairę.
Jei užrašytume mūsų medžius infiksine tvarka (kairysis pomedis, viršūnė, dešinysis pomedis), tada pirmas medis atrodytų taip: ((A, B, C), D, E), antras – taip: (A, B, (C, D, E)). Toks užrašymas gali padėti išsiaiškinti painius atvejus.

